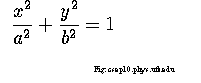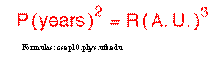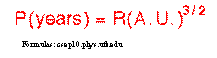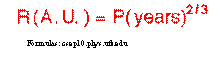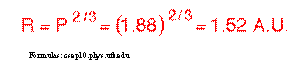Leanne Collins

While Kepler was working as an astronomer andmathematician in Austria, hewas required to compose an astrological calendar. On the calendar he includedhis predictions for a cold winter, and an invasion by the Turks. (At the timeof Keplerâs life, the studies of astronomy and mathematics were veryinterchangeable, and it was not at all unusual for a mathematician to create anastrological calendar.) When Keplersâ calendar was published, and hispre-dictions came true, the public went wild for him. He was revered by thepeople as a prophet, and for the rest of his life, he would turn to creatingastrological charts for extra income. (Kepler did not come from a wealthyfamily, and money was always a problem for him. His astrological charts allowedhim to continue his mathematical research and still collect a small amount ofmoney to survive on.) Kepler did not think particularly highly of theastrological pursuit, and, in fact, referred to it as ãthe foolish littledaughter of astronomy.ä (Hawking 629) He even felt that the public was equallyfoolish for holding it in such high regard. Kepler was quoted as saying ãif everastrologers are correct, it ought to be credited to luck.ä (Hawking 629)However, Kepler had no problem using the ãfoolishä pursuit to his ownadvantage, whenever money was tight. (In fact, he died while on a journey tocollect money from a chart he created.)

One day while Kepler was teaching, he drew on theblackboard a circle with an equilateral triangle inside of it. He then drewanother circle in the center of the triangle.It is said that the drawing was a revelation for him, and that it changed thecourse of his lifeâs journey. Somehow, from the drawing, he had the idea thatãthe ratio of the circles was indicative of the ratio of the orbits of Saturnand Jupiter. Inspired by this revelation, he assumed that all six planets knownat the time were arranged around the sun in such a way that the geometricfigures would fit perfectly between them.ä (Hawking 629) Kepler initiallytested his theory using two-dimensional figures (square, pentagon, triangle),but was unsuccessful. He then tested his theory using Pythagorean solids (cube,tetrahedron, dodecahedron, icosahedron, and octahedron) which are the only fivesolids that can be constructed from regular geometric figures. He reasoned thatwas why there were only six planets, because they had five spaces between them,and that the geometric figures explained the difference in the sizes of thespaces. From this theory, he wrote a book called Mysterium Cosmographicum (Mysteryof the Cosmos), which was published in 1596. As mentioned previously,Kepler agreed with Copernicusâ heliocentric theory of the planets revolving aroundthe sun. However, Copernicusâ theory had the sun somewhere near the middle ofthe orbits, but Keplerâs theory put it directly in the center. (Kepler wasdeeply religious and he was determined to understand how God designed theuniverse. Based on his beliefs, he placed the sun at the center of the orbit,and supported his theory by reasoning that God would have put the sun in themiddle because the revolution of the planets was central to Godâs design. Itturns out that Keplerâs theory was incorrect, but his conclusions wereaccurate, and played a large part in shaping the course of modern science.)

After Keplerâs book was published, he sent copies of it toother mathematicians and astronomers, such as Galileo and Tycho Brahe (awealthy Danish astronomer who held the position of Imperial Mathematician.)Galileo rejected the work because he felt it was speculative, but Tycho Brahefound Keplerâs ideas to be exciting. Brahe wrote to Kepler and invited him tocome to his castle in Prague,where he could continue to work on his research. It is said that Kepler was waryof Brahe, and was quoted as saying ãMy opinion of Tycho is this: he issuperlatively rich but he knows not how to make proper use of it, as is thecase with most rich people. Therefore, one must try to wrest his riches fromhim.ä (Hawking 631) Forever in pursuit of money, Kepler went to Prague towork with Brahe.

The relationship between the two men was tentative atbest. Kepler was allowed to assist Brahe with work that was portioned out tohim, but he was not allowed access to Braheâs extensive observational data.(This highly frustrated Kepler, who wanted to be treated as an equal, andallowed to do independent research.) Brahe had been studying the planet Marsand kept very detailed records of its movements. Brahe did not find popularityin his theories, but his careful research allowed Kepler to make furthermathematical distinctions regarding orbits and motion. Kepler continued tosearch for an explanation of the harmony and movements of the planets. Althoughstill deeply religious, Kepler did not allow religious dictations to force hismathematical computations into unnatural order (unlike Brahe.)

Kepler was eventually assigned to study the orbit of Mars,because it had an orbit that was not entirely circular, and that had been amystery to Brahe. Only a year and half into the working relationship, Brahebecame ill and died suddenly. Being promoted to Imperial Mathematician, andbeing quite the opportunist, Kepler quickly stole all of Braheâs data. Keplerhimself wrote ãI confess that when Tycho died, I quickly took advantage of theabsence, or lack of circumspection, of the heirs, by taking the observationsunder my care, or perhaps usurping them.ä (Hawking 631) Kepler stole thirtyyears worth of Braheâs planetary observations, and used the information tocompile his Rudolphine Tables (publishedin 1627.) Rather than continuing the work using the theories of Tycho Brahe,Kepler chose to use the data to support his own studies in predicting planetaryorbits. After eight years of continued research, Kepler was eventually able toprove that the work of Copernicus was incorrect in the theory that planetaryorbits were circular. Through his study of the orbit of Mars, he was able todiscover that the orbit was not just an irregular circle, but more importantly,that it was a precise ellipse. Kepler realized that all of the planetary orbitswere, in fact, elliptical. This discovery led Kepler to write the first two ofhis three laws of planetary motion, and in 1605, he announced them publicly.(In 1609, the first two laws were published in his book Astronomia Nova.)

Keplerâs first law of planetary motion is the law of ellipses:Ê

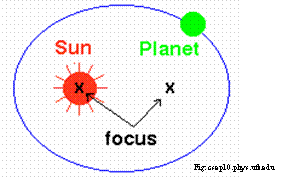
The above diagramshows that the sun is not at the center of the ellipse, but rather, at one ofthe foci. As the months change and the planet continues along its ellipticalorbit, its position changes from being closer to the sun, to being farther awayfrom the sun. This means that the Sun-Planet distance is constantly changing.

For any ellipse,there are two points contained within it called foci.Ê The sum of thedistances to the foci from any pointon the ellipse is a constant. The equation that defines the ellipse interms of distances a and b is:

a + b = constant

An ellipse is acircle that has been slightly flattened. The flattening of the circle isreferred to as ãeccentricity.ä When a circle is full, it has an ãeccentricityäof zero, and when the circle has become completely flattened into an ellipse,it has an ãeccentricityä of 1. Therefore the eccentricity of all ellipses lieson a scale between Zero and 1. (The elliptical orbit of a planet is only veryslight, and would not look as extreme as the egg shapes in the diagram below.)

ÊÊÊÊÊÊÊÊÊÊÊÊ ÊÊÊÊÊÊÊÊÊÊÊÊÊÊÊÊÊÊÊÊ ÊEquation for an ellipse:ÊÊ

Keplerâs second law of planetary motion is the law of equal areas:Ê

Keplerâs second law shows that because of the changein speed and distance affected by the orbit, the planet will cover equal areasin equal time. (The gravitational pull of the Sun will cause the orbit toaccelerate, allowing it to cover the same distance as it would when it is farthestfrom the Sun and moving slower.)

After Kepler published his first two laws, he was forcedto leave Prague whenit came under imminent threat of religious upheaval. Kepler returned to Austria, andin 1618 published Harmonies of the World,in which he detailed his third planetary law.

Keplerâs third law of planetary motion is the law of squares:Ê

Equationfor the ratio of squares:

Keplerâsthird law explains that the period of time that it takes for a planet to orbitthe Sun increases rapidly with the expanded radius of the planetsâ orbit. For example:The innermost planet of Mercury will orbit the Sun in 88 days, but in contrast,the outermost planet of Pluto will take 248 years to orbit
the Sun (see calculations following.)Ê

In the ratio ofsquares, the letter P represents theãperiod of revolution for a planetä and the letter Rrepresents the ãlength of its semimajor axis. The subscripts of ₁ and ₂ distinguishquantities for planet 1 and 2 respectively. The periods for the two planets areassumed to be in the same time units and the lengths of the semimajor axes forthe two planets are assumed to be in the same distance units.ä (http://csep10.phys.utk.edu)

ÊãThe long axis of the ellipse is called the major axis, while the shortaxis is called the minor axis.Half of the major axis is termed a semimajoraxis. The length of a semimajor axis is often termed the size ofthe ellipse. It can be shown that the average separation of a planet from theSun as it goes around its elliptical orbit is equal to the length of thesemimajor axis. Thus, by the "radius" of a planet's orbit one usuallymeans the length of the semimajor axis.ä (http://csep10.phys.utk.edu)

Followingare calculations using the third lawâs ratio of squares equation:

ãAconvenient unit of measurement for periods is in Earth years, and a convenientunit of measurement for distances is the average separation of the Earth fromthe Sun, which is termed an astronomical unit and is abbreviated asA.U.ä (http://csep10.phys.utk.edu) The denominatorsfrom the equation of the ratio of squares are equal, so the equation can berepresented as follows:

Thisequation can be solved for ãthe period P of the planet, given the length of thesemimajor axisä:

or it can be solved for the ãlength of thesemimajor axis, given the period P of the planetä(http://csep10.phys.utk.edu):

The followingis a calculation of the radius of the orbit of Mars (radius refers to thelength of the semimajor axis of the orbit.) The time for Mars to
orbit the Sun has been recorded as 1.88 Earth years. If we insert 1.88 into theequation where years are represented, the length of the semimajor axis for theorbit of Mars comes out to be 1.52 A.U. This answer (1.52 A.U.) has beenrecorded as being the exact measured average distance from the Sun to Mars.

Theplanet Pluto has been recorded to have an average separation from the Sun of39.44 Astronomical Units. If we insert 39.44 into the equation where A.U. isrepresented, the number of years turns out to be 248.

AfterKepler published his three laws, he proclaimed that they applied not only toMars, but to all planets, including Earth. In truth, Kepler never actuallyverified that any of his laws applied to other planets ö his proclamation wasjust conjecture. However, it turns out that he was right, and that his laws notonly apply to all planets, but also to comets, airplane flight, and satelliteorbits. Keplersâ work helped to prove that the theological explanation forcircular perfection was incorrect, and that the scientific idea of the orbitsbeing mystical no longer held true. In his time, Kepler had no way of knowingthat the mathematical laws of science were universal, and that one day theywould be readily accepted as truth.

Kepler never figured out why the planets move,but for the remainder of his life, he continued to search for the cause. Atsome point, Kepler vaguely touched on the notion that human bodies have amagnetic attraction, and extrapolated that the Sun may have an attractive forceon the planets in much the same manner. Kepler did not uncover the laws ofgravity in his lifetime, but he did pave the way for Isaac Newton to formulatehis theory of motion involving gravity as the cause of planetary motion.Keplerâs contributions to science did not receive much notoriety during thetime of his life, but his work has contributed greatly to the modern scientificage.

Works Cited

(credit:images, as noted.)

Hawking,Stephen.ãJohannes Kepler: His Life and Work.äÊ On The Shoulders of Giants. Ed.Stephen Hawking. Pennsylvania: Running Press, 2002.627-723

Kepler, Johannes. Harmoniesof the World, Book Five. Anapolis: St. Johnâs Bookstore, 1939.

http://csep10.phys.utk.edu/astr161/lect/history/kepler.html,03/20/04

(credit:image of Johannes Kepler on page 1 and other images, as noted.)

http://home.cvc.org/science/kepler.htm,03/20/04

(credit:images, as noted.)

http://story.news.yahoo.com/news?tmpl=story&cid=96&ncid=753&e=10&u=/space/20040317/sc_space/distantsednaraisespossibilityofanotherearthsizedplanetinoursolarsystem,03/27/04

http://mathworld.wolfram.com/EquilateralTriangle.html, 03/27/04

(credit:image, as noted.)