
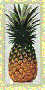






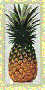





The Fibonacci sequence shows up in innumerable places in nature. Their occurrence is so frequent that it is difficult to know where to begin the descriptions. Since Fibonacci's original problem involving rabbits doesn't really work out (rabbits don't breed quite the way he imagined) does that mean that we can completely disregard his knowledge in small animal husbandry? The answer is "no." Fibonacci seemed to know what those rabbits and even bees were up to when they thought nobody was watching! It turns out that the numerical sequence described by the rabbit problem, is exactly the sequence of a bee's genealogy.
A male bee develops from an unfertilized egg, so it has only one parent. A female bee, on the other hand, develops from a fertilized egg, so she has two parents. Looking at the "Bee Family Tree" you will see the Fibonacci Sequence occurring in the male, female and total ancestors lines. The family tree below begins tracing the family tree with a female bee.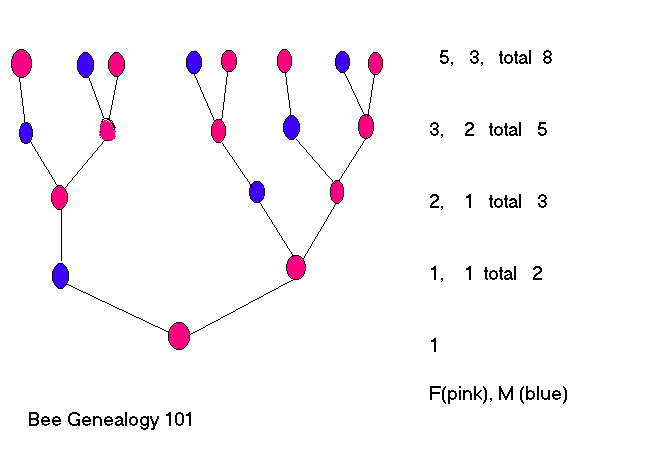
The number of petals on flowers as well as leaves on plants often occur as the Fibonacci Sequence. Phyllotaxis, the arrangement of leaves on a stem and in relation to each other, is not an absolute in all cases. It is definite in some plants (like iris and buttercups) and a strong likelihood in others. Here are a few examples:
3 - Lily, iris
5 - Buttercup, wild rose, larkspur
8 - Delphiniums, cosmos
13 - Ragwort, corn marigold, mayweed
21 - Aster, black-eyed susan
34 - Plantain, pyrethrums
The pattern of leaves, as they spiral up a stem, quite often occurs in the Fibonacci sequence. If the leaves of any plant grew in straight lines - directly above and below each other - then any leaf, or branch that was not at the top would have it's sunlight obscured by the leaves or branches above it. Expressed in the language of math, leaves do not occur 1/1, or every full circular rotation, but more often in phylloctactic ratios. Also called Fibonacci ratios, as their numerator and denominator are both generally Fibonacci numbers. Some example are:
2/3 - Grasses, elm
1/3 - Blackberry, hazel, fiddleneck
2/5 - Apple, plum, cherry, apricot
3/8 - Weeping willow, pear
5/13 - Bottlebrush, almond
One other place that plant life reflects the Fibonacci sequence is in the seed heads of numerous plants. The spiral pattern of the seed heads in both the clockwise, and counterclockwise direction, are quite often Fibonacci numbers. It appears that the reason for this formation is to allow the seedheads to pack the maximum number of seed in the given area. Some final examples:
5/8 - Pinecone
8/13 - Pineapple (the "eyes")
21/34 - Sunflower
A picture might make it a bit easier.
For some great Spiral Phyllotaxis pictures (that are all copyrighted) check out Scott Hotton's Phyllotaxis Page
Playing with the Numbers (Next)
Aesthetically Pleasing Fibonacci?