Go to MathDept Main Page | Go to MissionCollege Main Page

This paper was written as an assignment for Ian Walton's Math G -Math for liberal Arts Students - at Mission College. If you use material from this paper, please acknowledge it.

To explore other such papers go to theMath G Projects Page.
 

How many colors are required to color anymap so that no countries with common borders are the same color? It is generally held that four colors, for any flat map, willsuffice. But a belief that is commonly held and easily observed,is not a mathematical certainty. Nor does the simplicity of aquestion reflect the ease with which the answer can be proven.

The mathematical evidence to create a validproof that four colors are all that is required had evaded mathematiciansfor nearly 140 years. What became known as the Four Color Conjecturehas been the cause of great fascination and frustration. It hasalso been the stimulus for new ideas in topology, knot theory,and the concept of mathematical proof.

Historical Overview:

The question was originally posed by FrancisGuthrie, a former student of the famous mathematician AugustusDe Morgan, in 1852. Although Francis moved on to study law,his brother Frederick Guthrie had become a student of De Morgan. Francis Guthrie presented his work on the idea to his brotherasking that he pass it along to De Morgan.

De Morgan, unable to validate Francis Guthrieístheory, passed the problem along to Sir William Rowan Hamilton. The problem described by De Morgan to Hamilton was:

A student of mine asked me today to givehim a reason for a fact which I did not know was a fact - anddo not yet. He says that if a figure be anyhow divided and thecompartments differently colored so that figures with any portionof common boundry line are differently coloured - four coloursmay be wanted, but not more - the following is the case in whichfour colours are wanted. Query cannot a necessity for a fiveor more be invented.

Although Hamilton was unable to create a mapthat required five colors, he was also unable to prove that nosuch map existed.

In 1879 Alfred Bay Kempe publishes a proofusing an argument known as ìthe method of Kempe chains.î After more than twenty-five years, the Four Color Conjecturebecame the Four Color Theorem.

In 1890 The Four Color Theorem, once again,became the Four Color Conjecture when Percy John Heawood revealederrors in Kempeís proof. Kempe was unable to correct theseerrors.

Heawood continued to work on the problem,in various forms, throughout his life. He was a major contributorto the Four Color Theorem and itís eventual proof. Hedemonstrated that every map can be five colored as well as provingthat if the number of edges surrounding each region is divisibleby three, then the regions all require a maximum of four colors. His other contributions include what is now known as the ìHeawoodestimateî and notable advances in the study of number ofcolors required to color other surfaces (non-planar).

Overcoming the Difficulties of Proof

In 1879 a paper by Arthur Cayley was publishedby the Royal Geographical Society. It explained the difficultiesinvolved in attempting to provide a valid proof of the Four ColorConjecture. Evidence in this paper was undoubtedly abundant.

One of the most basic obstacles to be overcomein creating a valid proof is that there are infinitely many mapsthat can be drawn, and therefore infinitely many examples to betested. This is remedied through the use of proof through counterexamples. A counter example to the Four Color Conjecture wouldrequire that a map, within the parameters of the conjecture, becreated which required more than four colors.

In attempting to create counterexamples, itbecomes apparent that the shapes of the regions have little impacton the problem. It is the arrangement of adjoining regions thatis important.

This discovery allowed graphs to be used torepresent various map configurations. Placing a vertex at eachcapitolís border and then connecting the capitols of anycountries with a common border creates a graph. Using graphsalso allows configurations to be systematically created and analyzed,as required for a valid proof.

Although the original question is fairly clear,restrictions to create mathematical accuracy were added. In commonunderstanding these restrictions include the ideas that countriesmust be connected by regions, colonies spread across the map arenot to be considered.

Additionally a singleshared point does not constitute a common border. In this casemaps could be arraigned like wedges of a pie and would necessitateas many colors as wedges (regions). Figure 1.

Although I was unable to locate anything titledìTheorem 1," the two following Theorems are the mathematicaldescriptions of the conjecture to be proven. They also include,as a result of their preciseness, the restrictions noted above.

Theorem 2 of the Four Color Theorem states:ìEvery planar map with regions of simple borders can becoloured with 4 colours in such a way that no two regions sharinga non-zero length border have the same colour.î

Theorem 3 states ìEvery loopless planargraph admits avertex-colouring with at most four different colours.î

Modern Proofs

In 1976 two mathematicians at the Universityof Illinois, proved the Four Color Theorem (Theorem 3) throughthe use of computers. The proof achieved by Kenneth Appel andWolfgang Haken based their methods of reducibility on the Kempechains. Their methodology also utilized the ideas developed byHeinrich Heesch; the infinite set of maps could be constructedfrom a finite set of maps. Using a ìbuilding blockîconcept they constructed a set of 1500 unavoidable configurations. The details of the final proof were worked through using 1200hours of computer time. Initially this proof was met with someskepticism as it was the first proof which could not be verifieddirectly by ìhand.î This was a significant deviationfrom the traditional verification and validation process. Theavailable literature is somewhat ambivalent. Appel and Hakeníswork is referred to as a ìproof,î and the Four ColorConjecture is now noted as the Four Color Theorem, denoting somefinality in the problem. Yet despite independent verificationthrough computers and published details of the proof, it seemsthe proof continued to be held in lesser regards.

Despite the scrutiny and questions of it beingìsilicon proof,î the Appel and Haken proof was neverfound to be mathematically flawed. Yet the search for a methodicaland efficient, if not ìhandî verifiable proof continued.

Sometime in 1995, a new proof was presented. In the more compact and refined proof given by Neil Robertson,Paul Seymore, Robin Thomas and Daniel Sanders reference is madeto the Appel-Haken proof being ìnot completely satisfactory.î This cloud of doubt appears to be, at least in part, the motivationfor completing a new proof. The authors of the new proof alsoreference the history of disproved theorems to this problem anda desire to lay all questions to rest. According to the summaryof the Robertson, Seymore, Thomas and Sanders proof, not eventhe part of the Appel-Haken proof which is supposedly ìhand-checkableîhad ever been verified in its entirety due to its complexity andthe tediousness of the task.

The authors of the new proof indicate ìThebasic idea of the proof is the same as Appel and Hakenís.î Some of the key differences they note are:

The use of ìdischargingîfirstsuggested by Heesch.

A significantly reduced ìunavoidableîset size - 633 compared to 1476 set of Appel and Haken.

ìDischargingî method using 32rules where Appel and Haken used 300+

A quadratic algorithm to four-color planargraphs instead of a quartic algorithm

Only integer math was used to prevent roundoff and floating decimal errors.

(This information may be provided for justclarity, or in comparison to the Appel-Haken proof.)

Key Concepts in the Modern Proofs

One of the concepts used in the developmentof proof for the Four Colour Theorem was the use of the ìgreedyîor ìsingle mindedî algorithm. The purpose of analgorithm of this type is to perform a single task over and over(color the area of a graph) until it can no longer repeat thatsingle task.

The Kempe Method of chains is described bythe MacTutor Math online mathematics archive at Saint Andrews,in a document called ìThe Four Colour Theoremî asthe following:

If we have a map in which every regionis coloured red, green, blue or yellow except one, say X. Ifthis final region X is not surrounded by regions of all four coloursthere is a color left for X. Hence suppose that regions of allfour colours surround X. If X is surrounded by regions A, B,C, D in order, coloured red, yellow, green and blue then thereare two cases to consider.

(i) There is no chain of adjacent regionsfrom A to C alternately coloured red and green.

(ii) There is a chain of adjacent regionsfrom A to C alternately coloured red and green.

If (i) holds there is no problem. ChangeA to green, and then interchange the colour of the red/green regionsin the chain joining A. Since C is not in the chain it remainsgreen and there is now no red region adjacent to X. Colour X red.

If (ii) holds then there can be no chainof yellow/blue adjacent regions from B to D [It couldnítcross the chain of red/green regions] Hence property (i) holdsfor B and D and we change colours as above.

Graphs are created from maps by representingregions as vertices that are joined by edges if regions are adjacentresulting in a graph which is then ìplanar.î Areasof the graph are then ìtriangulatedî by adding edgesto any non-triangular regions. The set of configurations usedin the analysis for the proof are those parts of a traingulationscontained in a circuit.

Edges, vertices, triangles and other variationsare assigned numerical values and assigned degrees. Configurationsare then compared to determine if they are isomorphic.

Discharging rules involve assigning chargesto each vertex and redistributing. If the degree of the verticesis between 6 and 12 inclusively, it can be ìhand verified.î The others require the use of complex proofs written in formalcomputer language.

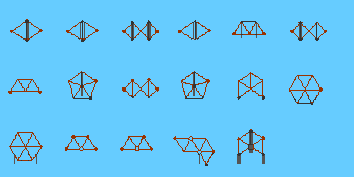
The 633 configurations used in the newestproof were all proven to be ìreducibleî which meansthat no configuration with this property can appear in a minimalcounter example. This concept was originally developed by Heesch. Figure below contains 17 of the 633 reducible figures from theproof summary. All of the figures used can be viewed by downloadingan ftp file at: http://www.math.gatech.edu/~thomas/FC/fourcolor.html#Algorithm

Summary

The Four Color Theorem has opened the doorto many coloring questions and answers. Mathematicians have proventhat the maximum number of colors required for any map drawn ona torus is seven and a double torus is eight. Carsten Thomassen,a graph theorist at the Technical University of Denmark, has demonstratedthat each type of surface, other than the plane, has a finitelist of maps that require six colors.

More importantly, The Four Color Theorem haschanged the way that mathematical proof is viewed. The Four ColorTheorem is the first proof that used a computer and was not actuallyable to be verified by hand. In the summary of the most recentFour Color Theorem proof the authors note:

In particular, we have not proved the correctnessof the compiler we compiled our programs on, nor have we havenot proved the infallibility of the hardware we ran our programson. These have to be taken on faith, and are conceivably a sourceof error. However, from a practical point of view, the chanceof a computer error that appears consistently in exactly the sameway on all runs of our programs on all the compilers... is infinitesimallysmall compared to the chance of a human error during the sameamount of case-checking.

As with the search for resolution of otherquestions in mathematics, the process of solving the Four ColorProblem opened the door to many new thoughts and ideas. One ofthose ideas is the use of computers to solve and prove mathematicalpuzzles that have yet to be resolved ìby hand.î Will the Four Color Theorem usher in a new form of proof? Itis hard to imagine otherwise. The use of a computer, and moreimportantly, the inability to verify and validate in the traditionalmethods, was met with resistance. But it also opens the doorto new and inventive ways to ponder other unresolved problems.

The internet, I believe, will also play aprofound role in the changing face of problem solving and validation. By placing the new Four Color Theorem proof on the internet,a proof which can be downloaded in less than twenty minutes, arethe authors in some way issuing a challenge?

The proof is now available for scrutiny, improvementas well as expansion of the ideas contained therein by the entireworld.

As limited as my mathematical experiencesare, I feel fairly certain, that the Four Color Theorem and computerproof, will prove as fuel for more questions, discovery and research.

Bibliography

ìAn Overview on Graph Theory.î Leibniz Laboratory, The Graph Theory Team

http://www-leibniz.imag.fr/GRAPH/english/overview.html (5/1/99)

Devlin, Keith. ìDevlinís Angle.î MAA online. September 1998.

http://www.maa.org/devlin/devlin_9_98.html(4/29/99)

ìKnot Theoryî Ideas, Conceptsand Definitions. MegaMath

http://www.cs.uidaho.edu/~casey931/mega-math/gloss/knots/knots.html(5/1/99)

ìProof, Mathematical,î MicrosoftEncarta 98 Encyclopedia. 1993 - 1997.

ìThe Four Colour theorem.î TheMacTutor History of Mathematics archive

University of Saint Andrews. September 1996http://www-history.mcs.st-andrews.ac.uk/history/HistTopics/The_four_colour_theorem.html(4/25/99)

ìThe Most Colorful Math of AllîMegaMath

http://www.cs.uidaho.edu/~casey931/mega-math/workbk/map/map.html(4/25/99)

ìThe Four Color Problem and its connectionto South African Floraî

http://www.uwinnipeg.ca/~ooellerm/guthrie/FourColor.html#Cayley(4/25/99)

Dr. Math. The Math Forum - Questions &Answers from our Archives. Articles:

Four Color Theorem 8/27/96 http://forum.swarthmore.edu/dr.math/problems/satyadeeppc.8.21.96.html(5/5/99)

Four Color Theorem 4/3/95

http://forum.swarthmore.edu/dr.math/problems/fourcolormap.html(4/29/99)

The Four Color Map Problem 11/12/97

http://forum.swarthmore.edu/dr.math/problems/lisa11.11.97.html(4/29/99)

Jenson, Tommy R. and BjarneToft. ìGraph Coloring Problems.î The Archive.

University of Southern Denmark 1/28/99

http://www.imada.sdu.dk/Research/Graphcol(4/25/99)

Peterson, Ivars. ìIvars PetersonísMathlandî. Science News Online. 1/4/97

http://www.sciencenews.org/sn_arc97/1_4_97/mathland.htm(5/1/99)

Robertson, Neil and Daniel Sanders, Paul Seymourand Robin Thomas.

ìThe Four Color Theoremî 9/13/95

http://www.math.gatech.edu/~thomas/FC/fourcolor.html#Algorithm(4/29/99)

Robertson, Neil and Daniel P.Sanders, PaulSeymour, Robin Thomas.

ìA New Proof of the Four-Colour Theorem.î

The American Mathematical Society Journal.

http://www-irma.u-strasbg.fr/EMIS/journals/ERA-AMS/1996-01-003/1996-01-003.html(5/1/99)

Miller, Charles D, Vern E.Heeren and E JohnHornsby, JR. Mathematical Ideas.

(8^th Ed.) Menlo Park: 1998

ìTopology,î Microsoft Encarta98 Encycolpedia 1993 - 1997.

Basic Concepts

Algorithm:

A precise, step by step problem solving procedure.

Conjecture:

Inference based on incomplete evidence.

Homeomorphic

Two figures or point sets are homeomorphicif a one-to-one correspondence that is continuous in both directionsexists between them.

Knot theory:

Branch of topology that deals with closedcurves that can be twisted and deformed in three dimensional space,but not torn.

Polynomial:

Any finite sum (or difference) of terms.

Proof:

Evidence or argument that establishes an assertionor conjecture as true.

Theorem:

A proposition in mathematics that has beenshown to be true.

Quadratic:

Of or containing quantities of the seconddegree.

Quadratic equation:

One variable is a polynomial equation of degreetwo.

Quartic Equation

Equation of the fourth degree - with a leadingterm of x^4.

Topology:

Branch of mathematics that explores propertiesof geometrical figures. Known as ìrubber sheetîor ìrubber bandî geometry. Concerned with relativeposition and general shape (as opposed to absolute position, parallellines and distance).

Triangulation:

To measure using trigonometry.

Trigonometry:

The study of relationships between the sidesand angles of triangles.

Graph Concepts

Complete graph:

A graph in which every pair of vertices isconnected by an edge.

Cycle/Circuit:

Path which begins and ends on same vertex.

Degree:

The degree of a vertex in a graph is the numberof edges that touch it.

Edge:

Lines connecting vertices.

Path:

Route traveled along edges.

Planar Graph:

A graph that can be drawn so that the edgestouch each other only where they meet at the vertices.

Size:

The size of a graph is the number of verticesthat it has.

Vertex, vertices:

a) the point at which the sides of an angleintersect

b) the point on a triangle opposite to andfarthest away from its base.

This paper was written as an assignment for Ian Walton's Math G -Math for liberal Arts Students - at Mission College. If you use material from this paper, please acknowledge it.