Go to Math Dept Main Page | Go to Mission College Main Page

This paper was written as an assignment for Ian Walton's Math G -Math for liberal Arts Students - at Mission College. If you use material from this paper, please acknowledge it.

To explore other such papers go to the Math G Projects Page.
 
 
 
 
 

Chaos, so whatáááá.So what is it? If I were nine years old again, I would say that it is anevil force of people fighting against the good forces of control. Now,if my question was based on the popular 1960's t.v. series, Get Smart,I would have been right, but my question deals with something a bit morecomplicated than a t.v. show. The chaos I will be discussing involves whatis technically known as non-linear dynamics, and in contrast to the previouslymentioned t.v. show, instead of chaos being the opposing system of control,it is simply a subset of the overall non-linear function of a system.

My goal for this paper is to define chaosin the most elementary way possible and still get the key points across.There is standard vocabulary when describing chaos that, I will define,so total understanding will not be so laborious (teacher excluded).

To best describe the name chaos, I wouldfirst say that "chaos" is clearly a scientific/mathematical oxymoron, justas "jumbo shrimp" is to food and not without reason. Even though the conceptof what we now call chaos is fairly new to the population in general, theroots of this phenomenon go way back to at least the 19^th century.Now that it has been definitively identified, people find it everywhere;in weather studies, fluid flow in rivers and large pipelines, traffic patterns,and biological behavior just to name a few. It happens that the availabilityof computer power makes possible many approaches to gaining some understandingof chaos that would not have been available fifty or sixty years ago. Thatis one reason why there is so much work going on in the area now.

To better understand the chaos theory, Ithought it might be helpful to define some keywords in relation to itsdescription. The underlying key to these words is that they are the conditionsinherent to the creation of chaos.

NONLINEAR

Lets begin with the definition for "nonlinear"since it is the actual essence of our subject matter (although not all-nonlinearpatterns produce chaos.) To understand a concept it is sometimes necessaryto define the opposite one, which is linearity. Linear equations in mathhave been used for centuries; the concept, set of instructions and resultsof an equation do not change in theory. In other words, we can rely onour knowledge of linear equations to solve applicable questions. A linearequation is one in which changes in initial variables produce equal changesin variables later in the process. Solutions display themselves by wayof straight lines on a graph. Linear equations aresolutions for cause and effect situations: a small cause yields a smalleffect, and a large cause yields a large effect. With all that said, Iwill describe nonlinearity. Nonlinear equations do not produce straight,somewhat predictable lines, but just as the name implies, these equationsproduce unpredictable line or shape patterns and move in any directionpossible. Nonlinear situations are more prevalent in our world than linearsituations. To explain this concept in a mathematical way, I will substitutethis quote, (5) "Mathematically, the signature ofa nonlinear system is the breakdown of the superposition principle whichstates that the sum of two solutions of the equation(s) describing thesystem is again a solution." What makes a nonlinear system difficult todetermine is the fact that any small disturbance in its already established,initial pattern can result in totally different behaviors of the systemat a time progressively later.

DYNAMIC SYSTEMS

A dynamic system is one of which is constantlychanging. Chaos can develop from regularity and regularity can developfrom chaos. This statement is an essential aspect of a dynamical system.In relation to the nonlinear concept, a dynamic system can be comparedto the movement of a pendulum, breaking wave or a rock rolling down thehill. In my work, telecommunications, a dynamic system can be related tothe traffic of calls utilizing different phone numbers and all sharingthe same T1 facility (24 call paths), randomly filtering through the systemon any one of those paths at any given time.

DETERMINISTIC

A deterministic system is, (3)"asystem in which later states evolve from earlier ones according to a fixedlaw." When applying this rule to an equation or explaining the processof a nonlinear movement, deterministic sequences are those that "decide"on a particular choice or path dictated by precise laws. In other words,a chaotic system may look random, but in reality, the deterministic lawsit follows are quite decisive.

ITERATIONS

Iterations describe a procedure present inchaotic systems. Iteration is simply repeating the same thing over andover. In working with fractal images its apparent that "self-referential"iterations occur to create the symmetry of a design.

SENSITIVE DEPENDENCE

"Sensitive dependence on initial conditions."This phrase is indicative of the sensitivity in changes related to chaoticbehavior that produce drastic differences. Weather is one area of studythat is very linked to this term. When experimenting, if initial conditionschange, even slightly, then the rest of the system takes a metamorphicturn, nowhere near similar to the system of the first initial condition.

BIFURCATION

An analogy of bifurcation can be shown bythe branches of a tree and by the complicated paths each branch takes toits point. Bifurcations are changes; changes in a system‰s behavior fromchaotic to more chaotic or steady to chaotic or chaotic to steady. Smalldisturbances will amplify and yield new behaviors. (1)"A bifurcation in a system is a vital instant when something as small asa single photon of energy, a slight fluctuation in external temperature,a change in density or the flapping of a butterfly's wings in Hong Kongis swelled by iteration to a size so great that a fork is created and thesystem takes off in a new direction." There is also a type of bifurcationthat is called "saddle-node" bifurcation. This is a label given to modesof behavior that cease to exist rather than become unstable.

PHASE SPACE & TRANSITION

The phase space is defined by the variablesof a mathematical equation plotted on a graph of multidimensions. Eachpoint on the graph displays the state of a dynamical system. Phase transitionis when the state of a system becomes drastically different, for example,when water boils or metal melts. The molecular structure takes on a stateof change. In phase transition, fluids become turbulent. The transitionis when order turns to chaos. Fractal geometry displays pictorially thechanges in a system.

BEGINNINGS OF A PHENOMENON

How did the discovery of chaos begin? Well,the concept of nonlinear systems did not exist in ancient times, but theconcept of chaos did. It was considered "formless matter" of complete confusion,existing before the universe. The Egyptians, Babylonians, Greeks and Romansall had comments about the fundamental ideas of creation, and with it,chaos. Chaos was always a force or entity related to order in a converseand counteracting way. Theological discussions of chaos began with thecreation of the universe, where chaos and order are reflections of God.

When Newton came along, mathematical equationswere applied to many systems of the world. Newton defined the laws of gravityand the law of motion. According to him, everything in the universe functionedlike a "well oiled machine", and was considered very predictable. He supportedthese ideas with differential equations that explain rates of change. Newtoncame up with a solution for the deterministic universe through linear mathematics.Newton did not know that future discoveries in math and nonlinear conceptswould prove his idea of the universe wrong. It took until the 19^thcentury for theories, defining chaos, to develop. A French mathematician,Jacques Hadamard, proved a theorem on the sensitive dependence on initialconditions. His examples used ideas from frictionless motion of a pointon a surface to geodesic flow on a surface with a negative curvature. AFrench physicist, Pierre Duhem, took to Hadamard‰s discovery and determinedthat, (6) "áprediction was ëforever unusable‰ becauseof the necessary present uncertain initial conditions in Hadamard‰s theorem."

Henri Poincare is the name most recognizedwith the application of nonlinear systems. In 1846, the planet Neptunewas discovered. Laws of Newton still prevailed. In 1889, the King of Norwayoffered a prize for the solution proving a stable universe. Poincare steppedup to the challenge and submitted his solution and won the prize, but anerror in his calculations required him to revisit his theory. (6)"In his 1890 paper, he showed that Newton‰s laws did not provide a solutionto the ëthree-body problem,‰ in other words, how one deals with predictionsabout the earth, moon and sun." This idea was not well accepted by thepowers that reigned at the time, because there was no definitive solutionto replace Newtons. Poincare was probing into equations as a result ofthe "three-body problem." He proved, through calculations that small gravitationalpulls from a third body might make another planet lose control in its orbitand behave unpredictably. Poincare uncovered that chaos is the essenceof nonlinear systems of which unpredictability reigns.

INTO THE 20^TH CENTURY

Up until the 1970s, computers were not widelyused, but existed. Before computers, all research involving chaos was achievedwithout the aid of mechanical processing from computers. Scientists, mathematiciansand physicists from around the world conducted experiments involving characteristicsinherent to chaos. Experiments in turbulence, period doubling, bifurcationand biological studies in population added to the understanding of chaoticorder. Two mathematicians from France, Pierre Fatou and Gaston Julia conductedresearch in the area of shapes, known as fractals. The two did not worktogether, but combined, their research covered much in the area of complexanalysis. By applying a calculus formula, Julia discovered that simplemappings of "many" or "complex" numbers led to intricate, complicated geometricshapes.

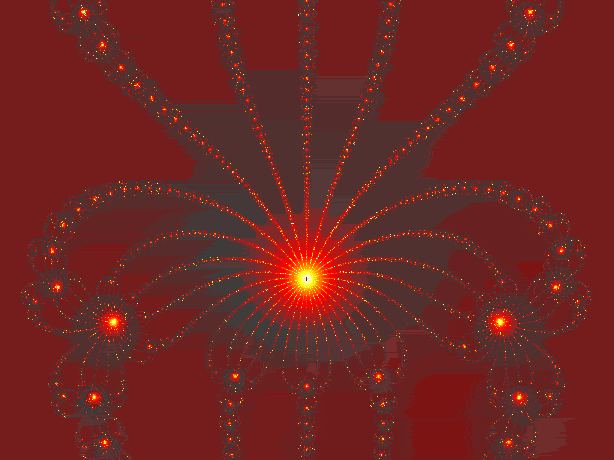
The birth of computers, no doubt, aided mathematicianBenoit Mandelbrot in his research of just about everything! In the 1960s,he began to realize that the culmination of his work in different areasproduced a common thread: a geometric structure, evolving from the dynamicsof nonlinear design that was soon to be known as a fractal. In the 70sMandelbrot was able to exploit his work through the use and aid of computergraphics, thus refining both his and the previous work of Julia and Fatou.Mandelbrot‰s work became so popular that the name, "Mandelbrot Set" refersto a specific set of points on a complex plane. A mathematical exampleof this set is described as follows, (13) "Pick apoint Z in the complex plane

Calculate: Z= Z + Z, Z= Z + Z, Z= Z + Z,Z= Z + Z

If the sequence Z,Z,Z,Zá remains within adistance of 2 of the origin forever, then the point Z is said to be inthe Mandelbrot Set."

Pictureof Mandelbrot Set

Also in the 1960s, an American by the nameof Edward Lorenz made discoveries that are now thought to be way aheadof his time. He deduced that nonlinear differential equations, in a finitesystem of deterministic nature, could describe and represent certain patternsin nature, mostly related to weather. Through the use of computers anddimensional representation of the phase space, Lorenz had demonstratedhis theory for all to see.

THE BUTTERFLY EFFECT

Even though all previous discoveries laida foundation for the phenomenon of nonlinear dynamics, only one event actuallyculminated all the theories into one; basically a new concept emerged calledchaos. The butterfly effect was the result of Lorenz‰s computer experimenton weather conditions. He made the significant discovery of how minutechanges in initial conditions changed the dynamics of a total given system,when stretched out over a long period of time. This was an accidental discoveryfor the man who was already ahead of his time. Applying his new discovery,he concluded that, conditions in weather that are forming in one directioncould take a drastic change and reinvent themselves into something entirelydifferent. This is the idea he coined the butterfly effect.

. http://library.thinkquest.org/26242/full/index.html

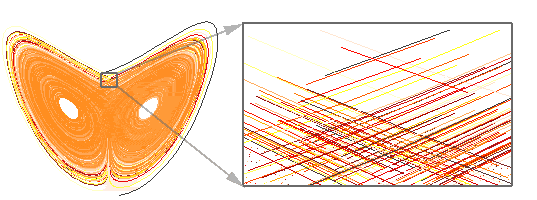
The Lorenz attractor-Although it might not seem so rightaway, this figure is a fractal since magnifying it does not decreasethe amount of detail:

FRACTALS

As Chaos began to gain new audience, it wasdiscovered to exist in many areas of our world. As mentioned earlier, Mandelbrotwas instrumental in defining fractals. The complicated mathematical formulasfor fractals create endless beauty and intrigue for the aesthetic observer.A factal is exactly what the name implies, a fraction or small chunk ofa larger, similar parent object. The fractal adheres to no scale, but whenviewed microscopically, the small patterns that make up the whole are commonlyreferred to as "self-similar‰ objects. If the scale of the object is iterateddown in size, the same object seems to appear, but in a rougher, more groovedform, just like many objects in nature. Geometric shapes appear in naturein the form of snowflakes, clouds, coastlines and mountains. Now computerscan simulate these fractals. Computerized pictures are produced on screenby mathematical formulas. A symmetrical formula produces a symmetric picture.Pixels on the computer screen follow the rules of a given formula and constructionof a beautifully colored geometric design unveil. So fractals consist ofthe same ingredients described for chaos. That is, dynamic movement withina determined environment based on sensitivity to initial conditions andpropelled by strange attractors. The symmetry created looks random andchaotic but it is not. Of course, there is much more to it than that, butagain, my goal is just to give a general description.

CHAOS IS EVERYWHERE

Weather, geometric structures in nature,and celestial systems all exemplify patterns of chaos. But there is more,chaos thrives in areas you might never have been aware of. The stock marketis one of those areas. Stock prices always appear to be random, and inthe short term they are, but continual observation has revealed long term,deterministic behavior.

In business organizations, chaos lurks asan insidious perpetrator. An example is in the Information Systems department.Historically, IT systems never quite repeat their past behavior, they arealways reinventing their structure, flourishing, dying off, and rebuilding.They exist amongst perpetual change to compensate for the unexpected.

Understanding chaos has also led modern medicineto apply its concepts to irregularities found in the heartbeats of patients.In addition, other biological and even theological studies have been madewith the use of this theory and I am sure more are to come.

CONCLUSION

Conditions of chaos may be distinct and applicationsof living chaos can be analyzed, but there is still an abstract characteristicof chaos that is hard to place in reality. To sum it up using my own analogy,I would say that chaos could be viewed as the space within a shoebox. Onthe outside, the box is defined by its rectangular shape, of known compositionand structure, but inside, the space could contain any number of ingredients,twisting and turning in what seems like unpredictability and randomness.These ingredients perform their bifurcations and iterations all withina determined structure, the box. Therefore, chaos lives within the structure.

Without chaos, our world would be boringand robotic. Any initial action would produce a common reaction. All ofnature could be predicted, so why would we need to think very hard? Ifall systems behaved in a methodical order, it would probably throw thebalance of the world off kilter. Ironically, it seems the presents of chaosultimately yield control!

1) Briggs and Peat. Turbulent Mirror, N.Y.: Harper and Row, 1989

2) Stewart, Ian. Does God Play Dice?, Massachusetts: Blackwell, 1989

3) Lorenz, Edward, N. The Essence of Chaos, Seattle: University of WA Press, 1993

4) Field and Golubitsky. Symmetry in Chaos, N.Y., Oxford University Press, 1992

5) Lam, Lui. Non-Linear Physics for Beginners, N.J.: World Scientific Publishing Co, 1998

6) www.wfu.edu/~petrejh4/HISTORYchaos.html

7) www.mwmbwrs.home.net/jason.yiin/content.html

8) www.cms.dmu.ac.uk/~nkm/CHAOS.html

9) www.santafe.edu/~gmk/MFGB/node2.html

10) www.life.csu.edu.au/complex/tutorials/tutorial3.html

11) www.easyweb.co.uk/~zac/chapt17.html

12) www.chaos.umd.edu/misc/poincare.html

13) www.library.thinkquest.org/3120/text.html