Math Department, Mission College, Santa Clara, California

Go to Math Dept Main Page | Go to Mission College Main Page

This paper was written as an assignment for Ian Walton's Math G - Math for liberal Arts Students - at Mission College. If you use material from this paper, please acknowledge it.

To explore other such papers go to the Math G Projects Page.

Hypatia of Alexandria

Math G

Midterm

Fall 2008

"Reserve your right to think, for even to think wrongly is better than not to think at all." Hypatia

Pythagoras, Euclid, Archimedes, Fibonacci, Descartes. What is the first thing you think of when you see or hear these names? Why math of course. These men are all famous mathematicians. They have contributed to mathematics as we know it today and their names are as recognizable as Michael Jordon’s….well…almost. Yet another thing that you may think when you see these names is that they are all men. How can that be? Granted, these men made great discoveries and were the trailblazers of their eras, but were there no female mathematicians in history? If there were, how come we never hear of any? Can it be that there were indeed none, and if there were a few, are they are not worth mentioning? In the United States we are struggling with attracting young women to the math and sciences, yet what we teach them, inadvertent as it may be, is that there is no history of women in ancient mathematics.

It is for this reason that I chose to write this paper on Hypatia of Alexandria. Hypatia as I will refer to her from her on, is thought to be the first female mathematician, teacher, philosopher and scientist.

The date of Hypatia’s birth is under debate, but the dates mostly given are between 350 and 370 AD. She was born to Theon, a great scholar and a professor at the Museum of Alexandria in Egypt. The Museum, at that time, housed the greatest collection of knowledge in the ancient world. Every ancient scientist, mathematician and philosopher spent time at the Museum in Alexandria. It is said that Theon passed on his love of knowledge to his daughter and she in turn surpassed him in intelligence and went on to become one of the ancient world’s foremost teachers and scholars, working in the fields of mathematics, astronomy and philosophy. She actually became head of the Neoplatonist schoolof philosophy around 400 AD. Students came from all over the world to be taught by her. She was revered by many of her students, but history shows that her most famous student Synesius of Cyrene, a Christian, was the one who revered her the most.

To the Philosopher (Hypatia) from Synesius;

“...But now your silence has been added to the sum of my sorrows. I have lost my children, my friends, and the goodwill of everyone. The greatest loss of all, however, is the absence of your divine spirit. I had hoped that this would always remain to me, to conquer both the caprices of fortune and the evil turns of fate”.(http://www.geocities.com/athens/acropolis/5164/sletter10.html, October 20, 2008, 4:05 PM)

It should not be overlooked that Hypatia herself was a trailblazer. Ancient Alexandria was very much a man’s world and the fact that she was accepted and respected by her peers speaks volumes to her intellect. She was best known for her eloquent style and her ability to simplify complex concepts. She never married and was a vowed celibate. Hers was a life full of knowledge, gaining it and transmitting it to others over that of a conventional wife and mother existence.

“She had self possession of manner, which she had acquired in consequence of the cultivation of her mind….she was admired on account of her extraordinary dignity and virtue.” (Socrates, Deakin, 2007, p. 55)

She wrote extensively, but most of her writings have been lost or destroyed. We know that she worked with her father, on commentaries on important texts, such as Ptolemy’s Almagest because he does cite her in his work. Historians also find it plausible that she had much more of a role in the rewriting of the Elements than previously thought.

“It is reasonable to hypothesize that Hypatia was involved. The extraordinary eloquence and clarity of the Elements that has been handed down to us suggests the hand of Hypatia” (Boyer, 1991, p 190).

Euclid’s Elements is thought to be one of the most influential textbooks in history. It is also believed that the version rewritten by Hypatia and Theo became the basis for all later editions.Many notable scientists including, Galileo and Newton were influenced by the Elements. As a matter of fact it is said that Newton’s interest in mathematics was “awakened” when he bought and read a copy of the book (Boyer, 1991, p 391).

A proof from Euclid's Elements that, given a line segment, an equilateral triangle exists that includes the segment as one of its sides. The proof is by construction: an equilateral triangle ΑΒΓ is made by drawing circles Δ and Ε centered on the points Α and Β, and taking one intersection of the circles as the third vertex of the triangle. (Wikipedia)

Euclid's Book 1 begins with 23 definitions — such as point, line, and surface — followed by five postulates and five "common notions" (both of which are today called axioms). Below are the five postulates.

1. A straight-line segment can be drawn by joining any two points.

2. A straight line segment can be extended indefinitely in a straight line.

3. Given a straight-line segment, a circle can be drawn using the segment as radius and one endpoint as center.

4. All right angles are equal.

5. If two lines are drawn which intersect a third in such a way that the sum of the inner angles on one side is less than two right angles, then the two lines inevitably must intersect each other on that side if extended far enough.

Example of 5th Postulate:

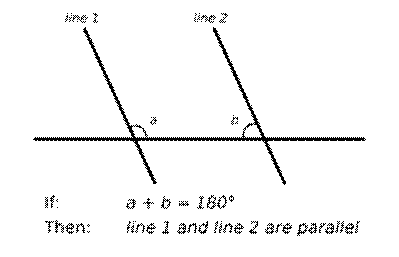
If the sum of the two interior angles equals 180°, the lines are parallel and will never intersect. (Wikipedia)

“There were four branches of mathematics in antiquity says Deakin (p. 59): arithmetic, geometry, astronomy, and music. The three works attributed to Hypatia by Hesychius cover one for one the first three of these. Of these four branches, we may see the first two as being “pure mathematics” and the others, astronomy in particular as being “applied.”

Most of the information we have on Hypatia comes from surviving letters of her most famous student, Synesius of Cyrene. Synesius was a neoplatonist like Hypatia and the most devout student of hers. Six letters and a fragment of a letter written to her survive. They have been translated to English by A. FitzGerald in The Letters of Synesius of Cyrene (London: Oxford University Press, 1926).

Synesius on many occasions, evident from his letters below, looked to Hypatia for advice and counsel. This in and of itself speaks volumes for Hypatia. That a man in the ancient world would seek counsel and guidance from a woman would have been unheard of had it not been that the woman was greatly respected and revered and perhaps even seen as an equal in matters of intelligence.

To the Philosopher (Hypatia) from Synesius:

“Concerning all of this I shall await your decision. If you decree that I ought to publish my book, I will dedicate it to orators and philosophers together. The first it will please, and to the others it will be useful, provided of course that it is not rejected by you, who are really able to pass judgement. If it does not seem to you worthy of Greek ears, if, like Aristotle, you prize truth more than friendship, a close and profound darkness will over shadow it and mankind will never hear it mentioned.” (http://www.geocities.com/athens/acropolis/5164/sletter154.html, October 20, 2008, 3:54 PM)

There is no real evidence that she partook in research mathematics, but it is evident from the letters of Synesius that her writings were meant to be learning tools and that she was intent on expanding the minds of her students while helping them to understand mathematics.

We do know that Hypatia authored a commentary called On the Conics of Apollonius, popularizing his text and developing the ideas of hyperbolas, parabolas and ellipses. She also authored a text entitled The Astronomical Canon, and she wrote a commentary on the first six books of Diophantus’ Arithmetica, including new original problems. Many agree that Hypatia was basically an algebraist who was inspired by Diophantus and that this was her greatest work. She lectured on the symbolism he had devised, the techniques he had developed and solutions to his problems. I will go over Arithmetica in greater detail later in this paper.

It is also believed, this belief derived from the letters of Synesius that Hypatia knew how to make hydroscopes and in fact constructed one for Synesius upon his request.

To the Philosopher [Hypatia] from Synesius:

“I am in such evil fortune that I need a hydroscope. See that one is cast in

brass for me and put together”.The instrument in question is a cylindrical tube, which has the shape of a flute and is about the same size. It has notches in a perpendicular line, by means of which we are able to test the weight of the waters. A cone forms a lid at one of the extremities, closely fitted to the tube. The cone and the tube have one base only. This is called the baryllium. Whenever you place the tube in water, it remains erect. You can then count the notches at your ease, and in this way ascertain the weight of the water.

(www.livius.org/su-sz/synesius/synesius_letter_015.html, Oct. 12, 2008)

Hypatia’s unfortunate death came at the hands of the Christians. It is said that although revered and respected by intellectuals, the Christians reviled her. Her belief in academicsand Greek scientific thought was in contrast to what the now in charge Roman emperors believed. Many also considered her a witch, due to her love of astronomy. As such, she could not be tolerated and a group of Christian zealots, stopped her chariot on the way home from the museum one night, tore her body to shreds and burned her remains.

“And in those days there appeared in Alexandria a female philosopher, a pagan named Hypatia, and she was devoted at all times to magic, astrolabes and instruments of music, and she beguiled many people through (her) Satanic wiles. And the governor of the city honoured her exceedingly; for she had beguiled him through her magic." John, bishop of Nikiu(http://cosmopolis.com/alexandria/hypatia-bio-john.html, October 21, 2008, 4:30 PM)

Her death marked the end of the age of great Greek mathematics. The museum was also eventually destroyed by the Arabs when they invaded Alexandria, thus basically ending western mathematics for a period of approximately 1,000 years.

A review of Hypatia’s achievements and legacy to mathematics:

· Diophantus’s Arithmetica

· Apollonius’s Conics

· Ptolemy’s Astronomical Works

Invented or helped invent the:

· Hydrometer

· Astrolabe

Together with her father, Theon, wrote commentaries on:

· Ptolemy’s Almagest

· Euclid’s Elements.

As I mentioned earlier, here we will review in more detail what is considered Hypatia’s most influential commentary: Diophantus’s Arithmetica.

Diophantus, often known as the 'father of algebra', is best known for his Arithmetica, a work on the solution of algebraic equations and on the theory of numbers.

The Arithmetica is a collection of 130 problems giving numerical solutions of determinate equations (those with a unique solution), and indeterminate equations. The method for solving the latter is now known as Diophantine analysis. Only six of the original 13 books were thought to have survived. There are many Arabic translations, for example by Abu'l-Wafa, but only material from these six books appeared. Heath writes in 1920:

“The missing books were evidently lost at a very early date. Paul Tannery suggests that Hypatia's commentary extended only to the first six books, and that she left untouched the remaining seven, which, partly as a consequence, were first forgotten and then lost."(www-history.mcs.st-and.ac.uk/printonly/Diophantus.htm, Oct. 13, 2008)

Some consider Diophantus’ work the most outstanding work on algebra in Greek mathematics and as we see above, had it not been for Hypatia’s commentary this work may very well have been lost.

Although Diophantus did not use sophisticated algebraic notation, he did introduce an algebraic symbolism that used an abbreviation for the unknown and for the powers of the unknown. As Vogel writes:

“The symbolism that Diophantus introduced for the first time, and undoubtedly devised himself, provided a short and readily comprehensible means of expressing an equation... Since an abbreviation is also employed for the word "equals", Diophantus took a fundamental step from verbal algebra towards symbolic algebra.”(www history.mcs.stand.ac.uk/printonly/Diophantus.htm, Oct. 13, 2008)

http://www.math.wichita.edu/history/men/diophantus.html, October 21, 2008, 5:55PM)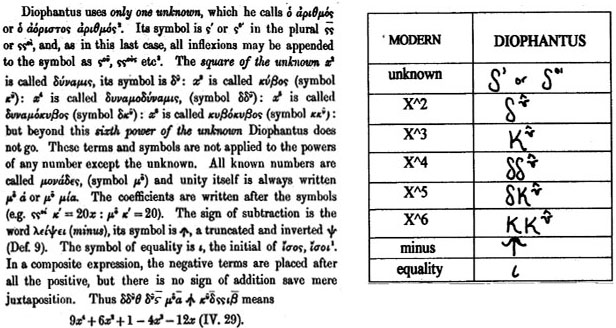

http://www.math.wichita.edu/history/men/diophantus.html, October 21, 2008, 5:55PM)

In the historical development of algebra, three stages exist: rhetorical (everything written out in words), syncopated (some representative symbols used), and symbolic. Diophantus introduced the syncopated style of algebraic writing, in which he could write polynomials in a single unknown.

http://www.math.rutgers.edu/~cherlin/History/Papers2000/kirschm.html)

An example of a problem from his works: Find 2 numbers such that the sum is 20 and the sum of the squares is 208. In terms of modern notation, the variables are:

(10 + x) and (10 - x); therefore, (10 + x)² + (10 - x)² = 208;and x = 2,

Today, Diophantine analysis is the area of study where integer (whole number) solutions are sought for equations, and Diophantine equations are polynomial equations with integer coefficients to which only integer solutions are sought. It is usually rather difficult to tell whether a given Diophantine equation is solvable. Most of the problems in Arithmetica lead to quadratic equations. Diophantus looked at 3 different types of quadratic equations:

ax2 + bx = c, ax2 = bx + c, and ax2 + c = bx

The reason why there were three cases to Diophantus, while today we have only one case, is that he did not have any notion for zero and he avoided negative coefficients by considering the given numbers a,b,c to all be positive in each of the three cases above. Diophantus was always satisfied with a rational solution and did not require a whole number which means he accepted fractions as solutions to his problems. Diophantus considered negative or irrational square root solutions "useless", "meaningless", and even "absurd". To give one specific example, he calls the equation

4 = 4x + 20

“absurd' because it would lead to a negative value for x. One solution was all he looked for in a quadratic equation. There is no evidence that suggests Diophantus even realized that there could be two solutions to a quadratic equation. He also considered simultaneous quadratic equations.

(http://www.math.wichita.edu/history/men/diophantus.html, October 21, 2008, 5:55PM)

Bibliograpy

Deaken, M.A.B., Hypatia of Alexandria, Mathematician and Martyr, New York, 2007

Zahm, Mozans, Women in Science: With an Introductory Chapter on Women’s Long Struggle for Things of the Mind, Appleton, 1913, Original from the University of Michigan, Digitized, July 20, 2007

Boyer, Carl B., A History of Mathematics (Second Edition), 1991, John Wiley & Sons

Online Sources:

http://www.geocities.com/athens/acropolis/5164/sletter10.html

http://www.math.rutgers.edu/~cherlin/History/Papers2000/kirschm.html

http://www.math.wichita.edu/history/men/diophantus.html

http://www.history.mcs.stand.ac.uk/printonly/Diophantus.htm

http://en.wikipedia.org/wiki/Diophantus

http://www.geocities.com/athens/acropolis/5164/sletter124.html

http://cosmopolis.com/alexandria/hypatia-bio-john.html

http://www.livius.org/su-sz/synesius/synesius_letter_015.html

http://www-history.mcs.st-andrews.ac.uk/Biographies/Hypayia.html