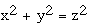
Go to MathDept Main Page | Go to MissionCollege Main Page

This paper was written as an assignment for Ian Walton's Math G -Math for liberal Arts Students - at Mission College. If you use material from this paper, please acknowledge it.

To explore other such papers go to theMath G Projects Page.
 

E. B. Burger

The evolution of Fermat's Last Theorem and the story of itssolution is a prime example of the challenge faced by mankindin his attempt to better comprehend the world around him. Thepursuit of methods of mathematics to solve scientific dilemmasis definitely more interesting than one might initially think. The following paper will highlight the pursuit of one of thebetter known mathematical fascinations of the last four hundredyears. The fascination takes on an added interest as it has recentlybe solved and heralded as a major breakthrough of the decade.

Pierre De Fermat was born August 20, 1601 in Beaumont Franceand educated at the University of Toulouse. He was born to anaffluent family, his father was a prosperous leather merchantand his mother was from a prominent family. This prominent statusmade a choice of a legal career typical of the time for someoneof his social and financial rank. His career progressed successfullyand he eventually obtained a position in the Parliament of Toulousein 1648. During the sixteenth and seventieth century the uniquenessof mathematics was representative of the individuals, goals andmethods each pursued. In the case of Fermat, with a career inlaw, the hobby of mathematics allowed him the freedom from thepressures to conform which law mandated. He did not depend onmathematics for his livelihood and held no career aspirationsas a mathematician as there were no positions to be gained withits exploration or discoveries. Personal gratification was theonly reward to be found. Perhaps as a result of this, Fermatwas reluctant to publish any his mathematical findings for fearhis hobby would no longer be enjoyable but a burden to prove. Fermat did correspond his mathematical theories with his otheracademic friends. If he had attempted to publish the lettersthat he circulated, he would have needed to labor over the methodologyand procedures of proof. Undoubtedly this would have turned thehobby into work. During his lifetime he only published one mathematicalpaper and that was an anonymous article.

Upon his death in 1665 his family and friends were concernedhis life long passion to gain further understanding of mathematicswould be lost forever. His son Samuel, also interested in thestudy and hobby of mathematics took up the task of collectingand publishing his notes. This was the forum where the famousFermat's Last Theorem came to be published. Around the year of1637 Fermat was studying the work of Diophantus of Alexandriaand its application to the area of number theory. His goal inhis research was to "renew arithmetic as Plato had understoodit, as the doctrine of whole numbers and their properties." To this end Fermat worked to develop a stricter method of mathematicalsolutions and disregarded the methods of Diophantus. Fermat'swork in the area of number theory resulted in creating a moremodern number theory. In the pursuit of number theory explanationshe worked primarily alone which resulted in much of the confusionfor future mathematicians. Because Fermat chose to work alonethere was no one to decipher his methods or notes. His notesat best were sketchy, if at all.

As Fermat was studying the theorem of Pythagoras' it leadhim to expand upon the idea of one of the best understood equationsin mathematics:

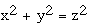
In any right triangle with shorter sides of xand y and thelongest side the hypotenuse z, theequation 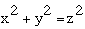will hold true. Pythagoras'stheorem is proof that there is a solution when n=2.

While Samuel was searching through Fermat's copy of Diophantushe found Fermat's Last Theorem written as a marginal note. Fermatwrote "I have discovered a truly remarkable proof which thismargin is too small to contain". His Last Theorem statesthat 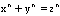has no non-zero integer solutionsfor x, y and zwhen n2.

Fermat claimed to know the solution not only in cubes but anypower greater that 2. Thiswas the challenge Fermat left to future mathematicians to solvewhen n>2. Since the solutionswas never written down the challenge was to remain unsolved forclose to four hundred years. Future generations were left toprove that there are no whole number solutions for the followingrelated equations:

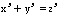
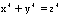
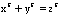
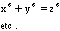
The difficulty in proving these equations is in the fact thatthere are infinite possibilities for the values of x,y, and z , aswell as infinite number of equations.

By the beginning of the 19th century,Fermat's Last Theorem had already become a challenging mathematicaldilemma to be solved in the area of number theory. Large prizeswere offered by Universities to anyone who could solve the infamousFermat's Last Theorem. This theorem has the distinction of beingthe theorem with the largest number of published false proofs. Apparently, over 1000 false proofs were published between 1908and 1912 alone.

The first major step forward in the solving of the Theoremwas to the credit of Sophie Germain who was born on April 1, 1776in France. Although her family was successful and financiallyable to enable her to pursue higher education her family did notbelong to the aristocracy to permit a woman to formally studymathematics. Sophie Germain's interest in mathematics came aftershe found a copy of book History of Mathematics, by Jean-Etiennein her father's study. In particular she read about Archimedesand the legend of his death. Archimedes was so consumed withthe study of a geometric figure in the sand he that he failedto answer a Roman soldier's question. His indifference was thecause of his death at the hands of the soldier. Sophie Germainfelt that mathematics must truly be fascinating for this legendto happen. Her interest in mathematics alarmed her parents asit was not a subject to be studied by ladies in the 1700's. Theyattempted to discourage her pursuits but failed and eventuallyher father funded her research and efforts. Her interest in numbertheory and calculus led her to teach herself the works of Eulerand Newton. For many years the only encouragement she would receivewould be from her parents. In 1794, the academy for mathematicaland scientific training was opened in Paris as a exclusively maleschool. Sophie resorted to posing as a former male student, Antoine-AugustLe Blanc, to enable her pursuit of her studies at the school. Each week she would submit the answers for the work under thename of Monsieur Le Blanc. She progressed well and unfortunatelyshe was found out through her brilliant answers. It seems MonsieurLe Blanc was known to the teachers for his lack of mathematicalabilities. The teacher, Lagrange, was astonished and pleasedto meet Sophie and became her mentor and friend in the pursuitof her studies.

Through Lagrange's guidance Sophie came to learn and becomeinterested in solving Fermat's Last Theorem. Sophie tried a newstrategy to the problem. Her initial goal was not to prove thatone particular equation had no solutions, but to make a conclusionabout several equations. In Sophie's attempt to prove the equationhad no solutions she developed what was to be know as the Germainprimes. Germain primes are those prime numbers, nsuch that 2n+1is also a prime number. Sophie's list of primes includes:

5 and 11since

2(5)+1=11

2(11)+1=23.

Both 11 and 23remain prime numbers (have no divisors other than themselves and1). Sophie went on to deduce that if nand 2n +1 are primes then thiswould mean that 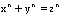implies that one of the x, y, zis divisible by n. With thisconclusion Sophie Germain proved Fermat's Last Theorem for alln 100 and eventuallythis was extended to all number less that 197. The Second possibility proposed was that only one of x,y, z is divisible by n. Sophie and mathematicians for her time had not proven for evenn=5 and this became the areathat future mathematicians concentrated on proving.

In 1847 significant progress was made in the study of Fermat'sLast Theorem when Lame announced to the Paris Academy that hehad proved Fermat's Last Theorem. His proof was the inspirationof Mathematician Liouville and suggested that the answer involvedfactorizing 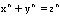intolinear factors over the complex numbers.

Liouville became best known for his work in fractional calculusand discovered transcendental numbers that removed the dependenceon continued fractions. Liouville built a infinite class of thesenumbers using continued fractions. The example he gave is nowknown as the Liouville number where there is a 1in place of n! and 0elsewhere:

.1100010000000000000000010000...

Liouville continued to work for the next several months to solvethe problem of unique factoring for these complex numbers. Liouvillefailed to prove the uniqueness of factorization, however thisfailure was instrumental to discoveries made by Kummer.

In 1856 Kummer presented the concept that when uniquenessof factorization failed it could be recovered by using ideal complexnumbers. With this new observation Kummer found examples whicha prime number is regular and proved Fermat's Last Theorem. Thecondition for a prime to be regular would be if the prime numberp does not divide the numeratorsof any of the Bernoulli numbers. The Bernoulli numberBn is defined by:

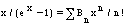
Kummer was able to prove that all primes up to 37 are regularwith the exception of 37 as it divides the numerator of 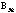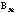. These discoveries of Kummer were essential in the solving ofFermat's Last Theorem since all later work for many years wasbased upon the thoughts of an ideal complex number. This introductionby Kummer led to the development of ring theory and much of explorationof abstract algebra.

Many historically prominent mathematicians attempted thesolution, only to fail to find the method to solve this mathematicalriddle. In their attempts many other significant mathematicalconcepts were realized. For nearly another one hundred yearsnothing of major significance would be developed in this area.

In 1955, Yutaka Taniyama was questioning and studying ellipticcurves and their relationship between properties of space healso made significant strides in solving the next piece of thepuzzle. As a result of his work on elliptic curves in the formof 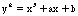for constants aand b. With assistance from mathematicians Shimuraand Weil a conjecture was developed to be known as the Shimura-Taniyama-WeilConjecture. In 1986 Frey made the announcement to the world thatthere was a connection between the 1955 conjecture and Fermat'sLast Theorem and was more than just an unsolved mathematical puzzlebut had fundamental importance to the properties of space.

To this point the solution to Fermat's Last Theorem had beenverified for specific equations but proof to the a general methodof solving the equation had not been presented. Princeton mathematicianAndrew Wiles made the commitment to solve the equation! Dr. Wileshad been fascinated with Fermat's Last Theorem since childhoodand this had been a deciding factor in the career choice of mathematics. In 1988 he began the task of providing the proof to the solution. He did not publicly make his search known but quietly workedaway in his attic office at home only telling a few trusted friendsof his intentions to solve the theorem.

In June 1993, Dr. Wiles gave a series of three lecturesat Princeton claiming the proof. Ironically, all but one studenthad dropped the course so when Dr. Wiles started the first dayof three lectures only one lone student student Nicholas Katzviewed his proof. By the third day of the lecture when word hadspread about the forthcoming proof all the lecture hall was packed. Having written the Theorem on the blackboard he claimed to havesolved the Last Theorem and would stop there. Dr. Wiles had notonly proved the Shimura-Taniyama Conjecture he had provided examplesto prove Fremat's Last Theorem. Dr. Wiles sent his careful researchfor review to a select group of experts in the field of mathematics. Having spent so much time on his work he wanted to ensure hisproofs were secure and fix any problems before formal publication.

In the fall of 1993 some minor mistakes were fixed but alarger hole in the method was found and unable to easily be fixed. For the next six months Dr. Wiles worked in collaboration withDr. Taylor of Cambridge University to find the missing pieces. The new insight came in a method to allow a infinite collectionof mathematical objects called Hecke rings to be constructed. They used the idea to take one element of a set and use thatto find the next element, then to use the second construct thethird and so on.

Dr. Wiles work has been described as the greatest advancesyet and decades beyond the predicted time-line for solving theTaniyama conjecture and proving Fermat's Last Theorem. Aftercompleting the written documentation to his proof Dr. Wiles retiredfrom the Taniyama project.

The pursuit of Fermat's last Theorem has captivated thousandsof professional and amateur mathematicians throughout the ages. In researching this paper and attemping to comprehend the mathematicsinvolved has proved to be suprisingly interesting. This has providedme with a greater appreciation for the intensity and dedicationwith which these academics have devoted to solving the great mathmaticalmysteries.

This paper was written as an assignment for Ian Walton's Math G -Math for liberal Arts Students - at Mission College. If you use material from this paper, please acknowledge it.