
 Math
Department, Mission College, Santa Clara, California
Math
Department, Mission College, Santa Clara, California
Go to Math Dept Main Page | Go to Mission College Main Page
This paper was written as an assignment for Ian Walton's Math G -
Math for liberal Arts Students - at Mission College. If you use
material from this paper please acknowledge it.
To explore other such papers go to the
Math G Projects Page.
This report was submitted by Jessica Kahlich for her Fall 2008 Math
G Midterm at Mission College
Practical Mathematics for the Aspiring
Time Traveler
Jessica Kahlich
Math G
Ian Walton
10-26-2008
It may seem the stuff of science fiction, but time travel is something
that already affects our day to day life. Humans have been able to look
years into the past for generations, and we have already successfully
time traveled into the future. The men behind the math for time travel
are respected scientists such as Albert Einstein and Kurt Gödel,
not the fictional authors one might expect. Instead of phone booths or
DeLoreans with flux capacitors, the foundations of theoretical time
travel are practical and are based around gravity and the bend of
spacetime. Spacetime is defined as the fabric of space and time that is
warped by the gravitational forces of objects.
Before Einstein’s general theory of relativity, Newton’s laws of
gravitation did not account for some of the anomalies in the
gravitational orbits of planets nor did it allow for the concept of
time travel.
From Newton
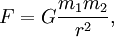
to Einstein
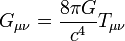
Einstein field equations are more complicated and accurate shown here
in “simplified” formula form, which is used to calculate how mass and
energy create the curvature of spacetime. The tensor formula is
Gμν (metric tensor or gravitational field) is equal to 8πG (gravity)
over c4 (speed of light to the fourth power) times Tμν (stress-energy
tensor or the cause of the gravitational field instead of mass in
Newton’s formula). This is important because Einstein’s theory
has become a cornerstone of astrophysics, molds our understanding of
black holes (which is later explored in the idea of time travel), and
the big bang theory. Einstein’s field equations would later be solved
by Kurt Gödel into a theory of spacetime that would prove the
equations allowed for time travel into the past. Though ultimately
proved flawed, Gödel’s model was the start of an interest in the
scientific community for real solutions to the question of time travel.
Now establishing that theoretically time travel is possible, it must be
further broken down into two distinct types of time travel- traveling
to the past and traveling to the future. We look into the past every
day. Due to the speed of light we see things as they were when the
light was originally transmitted to us. For most interactions this is a
nanosecond of looking into the past, but when it comes to looking to
the stars we are seeing years into the past, and with the use of
telescopes millions of years. A light-year is a unit of length
and describes how long it takes for the light to emit, and transmit
across the vacuum of space. The light we are looking at from the
closest star in the constellation Orion actually took 26 years to reach
our planet, so we are consistently viewing it as it was 26 years ago.
How far away is it in distance? Each light year is 5,878,625,373,183.61
miles away.
While we are able to easily look into the past, time traveling to the
past is a complicated idea. There are several theories including faster
than light and closed time like curves like those in the solution by
Kurt Gödel, but neither so far has been proven even theoretically
possible. Another theoretical solution is a traversable wormhole, but
no examples of such wormholes exist. Theoretically one could also build
a time machine using cosmic strings, or the texture of spacetime, but
one could never travel back before the time machine was built. This is
how some scientists explain why we have never been visited by time
travelers, but still insist that time travel is possible.
In contrast to how theoretical and complicated time travel to the past
is, time travel to the future has already been achieved. Cosmonaut
Sergei Avdeyev currently holds the record for the most time traveled
into the future: 20 milliseconds. His missions on the Mir Space Station
kept him in orbit for over 748 days. How that traveled him into the
future can be explained by Einstein’s theory of special relativity,
which contains the idea of time dilation. The concept of time dilation
is that a clock ticks slower in movement as opposed to a stationary
clock; the faster the moving clock is going the slower it will tick.
During Avdeyev’s time on the space station he traveled at 17,000 mph
and was thus propelled into the future. Though this is a small amount
of time, it does prove that time travel into the future is possible.
For the time dilation method of going into the future 88 miles per hour
in your car is not going to be fast enough to be noticeable. Speed is
the key. The closer to the speed of light you are, the more time will
pass on earth in direct relation to less time passing from your
perception while you are traveling back and forth.
To figure out how fast you need to go to get to your desired point in
the future, this time dilation formula is handy. 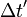 (time between
two events from 1st observer, time traveler) is equal to γ (the Lorentz
factor) times
(time between
two events from 1st observer, time traveler) is equal to γ (the Lorentz
factor) times 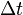 (time between concurrent
events from 2nd observer, earth) is equal to
(time between concurrent
events from 2nd observer, earth) is equal to 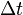 (time between
concurrent events, earth) over the square root of 1 -
(time between
concurrent events, earth) over the square root of 1 - 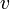 2 (velocity
between stationary measurer and moving clock squared) over
2 (velocity
between stationary measurer and moving clock squared) over  2 (speed of
light squared). This formula shows the moving clock’s or you the time
traveler’s duration to be increased, so the faster the moving clock is
going the more the duration is increased, thus making it seem to tick
slower. Black holes where the fabric of spacetime is bent and slowed
would be a more fuel efficient way to travel via this method.
2 (speed of
light squared). This formula shows the moving clock’s or you the time
traveler’s duration to be increased, so the faster the moving clock is
going the more the duration is increased, thus making it seem to tick
slower. Black holes where the fabric of spacetime is bent and slowed
would be a more fuel efficient way to travel via this method.
Time dilation remains the only successful method to time travel to the
future, but there are of course other theories. These theories employ
devices including using cosmic strings and rings with light at near
zero temperatures. Were these devices to work there are a few more
factors to consider. While time dilation and traveling through worm
holes both involve movement to achieve time travel, these devices are
either stationary or are on the earth’s crust. Add time travel into the
equation and there are two small problems: 1) finding where you are as
a stationary object and 2) “landing” on the earth that is not
stationary.
s2 = x2 + y2 + z2 – (ct)2
So how do you find out where you are in these dimensions? The
Pythagorean theorem with Einstein’s relativity theorem make this
equation for spacetime version of gps. s2 (spacetime
squared) is equal to points x2 + y2 + z2 minus c (speed of light) times
t (time) squared. So now that you know where you are, you’ll need to
account for five things: rotation, tilt, “wobble”, inclination, and
orbit. Accounting for all five is necessary to make sure you don’t end
up in the earth’s crust or core, on or in the moon, or just hanging out
in the middle of the vacuum of space.
Earth’s rotation is currently monitored by telescopes and satellites,
but it is still hard to measure due to variability and the gravity
generated by the other orbiting planets. Still earth rotation
information is available through several sources. Earth’s tilt is
23.44° and remains fixed in the same direction, however there is
some variance in the tilt and it can move from 22.1° to 24.5°.
Although it is a slow process, the wobble of the earth over precession
is enough to affect anything on its surface remaining at a fixed point.
The wobble refers to the gyroscopic movement of the earth due to its
wide belt and tidal forces. Finally the orbit of the earth in space can
be calculated by Kepler’s laws of planetary motion, but the inclination
of the orbit must be included in these calculations. So the orbit of
the ellipse 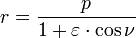 must take into account the
inclination
must take into account the
inclination 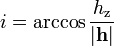 .
.
There are many factors a stationary device, if possible, must overcome
in order to propel itself into a point in the future that is sure
to land you on solid ground. Science fiction may have the idea of a
time machine device oversimplified, but time travel is possible. In its
current form we can see into the past and we have had astronauts and
cosmonauts travel into the future. While it might not be the magic of a
push of a button, there is already a proven way to travel even further
into the future. Time travel is all around us already, who knows where
it could go tomorrow. The science is there for those eager enough to
parse out the complications of Einstein’s relativity and already ready
for those with the need for speed and equipped with a towel.
References
Books
Bennett, Jeffrey, Megan Donahue, Nicholas Schneider, and Mark Voit. The Essential Cosmic Perspective.
4th ed. San Francisco: Pearson Addison-Wesley, 2008.
Jagerman, MD Louis S. The
Mathematics of Relativity for the Rest of Us Trafford
Publishing, 2001
Gott, J. Richard. Time
Travel in Einstein's Universe: The Physical Possibilities of Travel
Through Time Mariner Books, 2002
Article
Cho, Adrian. (2003) Einstein 1, quantum gravity 0. (Spacetime, studies
of gamma rays suggest that the Lorentz invariance holds, and that space
and time are smooth at small scales). Science,
p1169.
Websites
http://nostradamus.time-loops.net/Einstein.htm
http://en.wikipedia.org/wiki/General_relativity
http://en.wikipedia.org/wiki/Speed_of_light
http://en.wikipedia.org/wiki/Time_travel
http://en.wikipedia.org/wiki/Theory_of_Special_Relativity
http://en.wikipedia.org/wiki/Time_dilation
http://en.wikipedia.org/wiki/Lorentz_factor
http://www.scifiscience.co.uk/themes/timetravel/detailed.html
http://www.cv.nrao.edu/~rfisher/Ephemerides/earth_rot.html
http://www.abc.net.au/science/slab/wormholes/default.htm
http://en.wikipedia.org/wiki/Kepler%27s_laws_of_planetary_motion
http://www.iers.org/MainDisp.csl?pid=95-84
http://vinkovic.org/Projects/PopularScience/Gott_interview/J.Richard.Gott.III.eng.html
Cover Image from xkcd.com
Images from Wikipedia.com


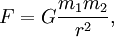 to Einstein
to Einstein 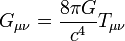
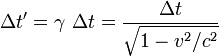
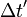 (time between
two events from 1st observer, time traveler) is equal to γ (the Lorentz
factor) times
(time between
two events from 1st observer, time traveler) is equal to γ (the Lorentz
factor) times 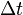 (time between concurrent
events from 2nd observer, earth) is equal to
(time between concurrent
events from 2nd observer, earth) is equal to 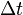 (time between
concurrent events, earth) over the square root of 1 -
(time between
concurrent events, earth) over the square root of 1 - 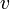 2 (velocity
between stationary measurer and moving clock squared) over
2 (velocity
between stationary measurer and moving clock squared) over  2 (speed of
light squared). This formula shows the moving clock’s or you the time
traveler’s duration to be increased, so the faster the moving clock is
going the more the duration is increased, thus making it seem to tick
slower. Black holes where the fabric of spacetime is bent and slowed
would be a more fuel efficient way to travel via this method.
2 (speed of
light squared). This formula shows the moving clock’s or you the time
traveler’s duration to be increased, so the faster the moving clock is
going the more the duration is increased, thus making it seem to tick
slower. Black holes where the fabric of spacetime is bent and slowed
would be a more fuel efficient way to travel via this method.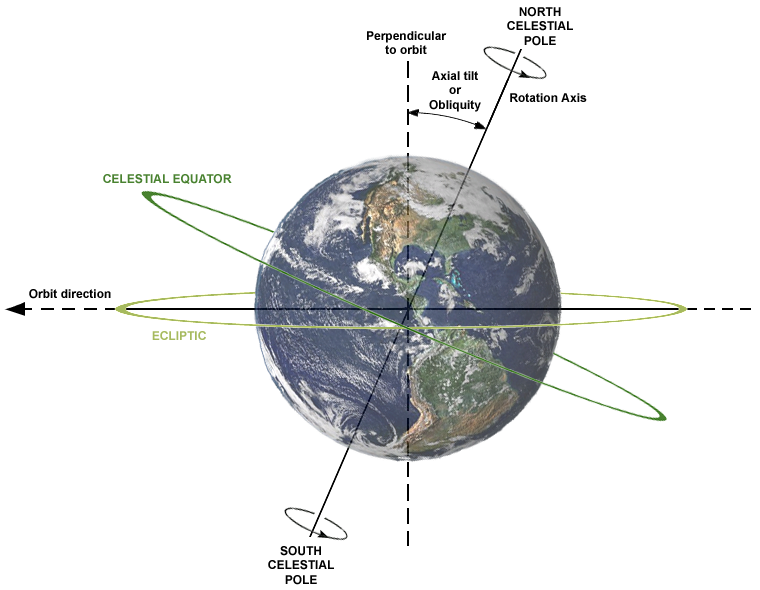

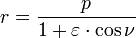 must take into account the
inclination
must take into account the
inclination 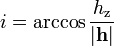 .
.