The Golden Mean
I remember the first time I heard about the Golden Rectangle. I was taking a high school art appreciation class and the instructor was explaining the importance of the Golden Mean in the arrangement of elements within classic paintings by masters such as Leonardo Da Vinci and in classic architecture like the Parthenon in Greece. What eluded me was how this arrangement was created and how it came to be. Unfortunately, I only learned that this was an important technique used by the masters and heard not a word on how to create this proportion and use it to improve what I might aspire to create.
I thought I had completely forgotten that lesson until I had the opportunity to select a topic of my own choosing for my math class. Seemingly, from out of nowhere, this topic came to mind. All my curiosity about this mysterious concept returned. I knew that it had to contain some math since it was a proportional ratio. What I had not counted on was how dependent on math the Golden Mean really is. I had no idea that I was in store for a tour through a number of complex and fascinating math concepts that all contributed to what, on the surface, appeared to be a simple idea.
The Golden Mean has been recognized as the "Divine Proportion" and has been used as the blueprint for great works of art and classical architecture. There is even speculation that great music composers such as Mozart have used the properties of the Golden Mean in the creation of some of their music. In fact, the Golden Ratio is so plentiful in nature that we unknowingly see examples of it around us everyday but before one can understand what the Golden Mean is, it is necessary to understand mathematical concepts such as the Fibonacci Sequence, Phi, and their relationship to our perception of beauty.
The simple definition of the Fibonacci Sequence is a sequence of integers in which the value of a number at any position is the sum of the two numbers preceding it. Of course, there is the exception of the first position since it has no numbers preceding it (figure 1).
figure 1. The Fibonacci Sequence
Interestingly, the sequence was discovered as a solution to a problem Fibonacci explored in his book, Libor Abaci, written in 1202. The problem is described by the need to determine how many rabbits would be born to a single breeding pair during the period of one year. The limitations (restrictions) of this were that the rabbits could not reproduce during the first month since they were not yet sexually mature and every offspring pair would reproduce in the same manner, bearing one male and one female that would, subsequently, repeat the cycle after the maturation period. Obviously, this was an unlikely outcome due to the predetermined outcome of the offspring. However, the question itself remains valid. Fibonacci's solution to this problem was a numerical representation of exponential growth. The sequence yields some interesting patterns when studying the relationships between the numbers in the sequence. One behavior is that there is always a difference of exactly 1 when applying the following formula: Square any number in the Fibonacci Sequence, excluding the number 1 in the first position, multiply the numbers occurring immediately on either side of the chosen number, subtract the smaller number from the larger. The difference will always be the number 1 (figure 2).
- F142
- 3772 = 377 x 377 = 142,129
- F13 x F15 = (233 x610) = 142,130
- 142,130 - 142,129 = 1
figure 2. Pattern Example
Another interesting behavior occurs when you divide any number except the first few by the number preceding the selected number. The result will be the "growth" ratio of the sequence. This ratio is Phi (1.6180339) and is represented by the Greek letter Ø (figure 3).
F15/F14 = 610/377 = 1.618037
F40/F39 = 102334155/63245986 = 1.618033988
Phi Ø = 1.618033989
figure 3. Phi
F40/F39 = 102334155/63245986 = 1.618033988
Phi Ø = 1.618033989
figure 3. Phi
Phi also happens to be the "Golden Ratio". The result of this division is always a closer approximation to Phi when you calculate higher positions of the sequence. Calculating higher Fibonacci numbers requires the use of a computer since these numbers can quickly reach hundreds and even thousands of digits in length. This is a result of the Fibonacci sequence being an infinite sequence (aleph null). Regardless of the numbers in the sequence that are calculated, the result will always be closer to Phi alternating between being slightly higher or slightly lower than Phi as you calculate higher numbers in the sequence.
Before moving on to describe the relationship the Fibonacci sequence has with the Golden Rectangle, it is first necessary to understand a bit more about Phi. As I stated earlier, the value of Phi is 1.6180339 (figure 3). Proof of this is in the quadratic equation shown in figure 4.
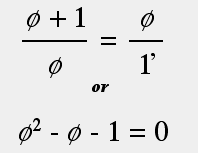
figure 4. Quadratic formula
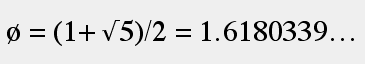
figure 5. solution for Quadratic formula
From figure 4 we get the solution listed in figure 5.
Now that we have proof that Phi = 1.6180339, what is its significance? Simply stated, Phi is the ratio of an additive sequence. In itself, this statement may be confusing. However, once one becomes aware of the many examples around us that incorporate an additive sequence, it is virtually impossible to ignore the presence of Phi. The Golden Ratio is prevalent in art, architecture, music, and nature. It is the occurrence of Phi in nature that has influenced the endeavors of man but also earned it the title as the Divine Proportion since it appears to be the favored ratio of growth in nature. One of the most well known examples of the occurrence of Phi in nature is illustrated in the bisection of a chambered nautilus (figure 6). An example familiar to most classically trained artists is that of the Golden Rectangle (figure 15).

figure 6. Chambered nautilus
The form of the Golden Rectangle is said to be aesthetically more pleasing than the equally proportioned square. This belief has sparked a great deal of controversy as I will explain later. Regardless, the Golden Rectangle has been the mainstay of aesthetic beauty used by the ancient Greeks, Leonardo Da Vinci, and countless other artists through the ages. The Golden Rectangle is created by dividing a line or segment into extreme and mean ratio with the length of the sides being equal to the mean length. The following illustrations will show the construction of a Golden Rectangle (figure 7 - figure 13).
figure 7. | Start with a square (all sides being equal) | |
figure 8. | Bisect the square vertically into two equal parts. The values of each being 1/2 of their previous value. | |
figure 9. | Draw a straight line from the center point on the bottom of the square to the upper right hand corner. The line is determined by using the Pythagorean Theoreum: the sum of the squares of the legs of a right triangle is equal to the square of the hypotenuse a2+b2=c2 | |
figure 10. | Using the line created from figure 9 to serve as the radius of a circle. | |
figure 11. | Extend the line from the bottom of the square to the point where the circle intersects with it. | |
figure 12. | Repeat steps in figures 9-11 for the top (invert the procedure) | |
figure 13. | Draw a straight line to connect the end points where the top and bottom of the square were extended to create a Golden Rectangle. | |
| Figure 14 shows an example of a completed Golden Rectangle which clearly shows the 1 to 1.6180339 ratio. However, there exists an additional relationship in which the mean ratio of c becomes the extreme ratio and takes the place of b in the subdivision. By applying some of the steps in the previous examples to the subdivision we can continue the process within the rectangle. | ||
| figure 14. | ||
figure 15. Equiangular spiral
figure 16. Parthenon illustration w/Golden Rectangle overlay
In addition to existing in nature, art, and architecture, it has been hypothesized that great classical composers like Mozart had an awareness of the Golden Ratio and used it to compose some of his famous sonatas. Surprisingly, the Golden Ratio appears in a couple of different aspects of music. It appears in particular intervals in the western diatonic scale as well as the arrangement of a piece of music itself. In order to clearly understand the relationship between the Golden Mean and music, it helps to have a working knowledge of the fundamentals of western music theory and a basic knowledge of sound. The Golden Ratio appears in the relationship of the intervals or distance between the notes. Each of these intervals or note pairs creates either a tonic (consonant) sound or a dissonant sound, in which the listener desires to hear it followed by a tonic sound to "resolve" the tension created by its unstable quality. The interesting part of this, according to H.E. Huntley, author of the Divine Proportion, is that it is a relationship of the consonance and dissonance of the rhythmic "beats" that occur in the sound waves of the resonant frequencies between notes in the diatonic scale. Huntley goes on to explain that the reason that we prefer visual aspects of a Golden Rectangle over a perfect square is measured in the amount of time it takes for the human eye to travel within its borders. This period of time is in same proportion (Phi) to the beats that exist in specific musical intervals. A Unison (two notes of the same frequency being played simultaneously) is said to be the most consonant, having a rhythmic quality that is similar to the time interval that is perceived by the eye when viewing a perfect square. The octave has a similar consonant quality that could be represented visually by two squares of equal size. A correlation could be made between the consonant properties of the interval of an octave to the first two squares in the golden rectangle or the first two numbers in the Fibonacci sequence which are represented as 1,1. From there the relationship reflects a ratio of 8:5 in the interval of a Major 6th (an approximate Golden Ratio of 1.6), in the first and sixth notes of a diatonic (Major) scale. The ratio of this interval is related by the rhythmic beats that are created by the respective frequencies of the sound waves and interpreted as sound in the human ear. Suffice it to say, that the interval of a Major 6th is supposed to be the most aesthetically pleasing since it contains the golden ratio.
Another aspect of the golden ratio in music is illustrated in compositions by Mozart. Mozart's piano sonatas have been observed to display use of the golden ratio through the arrangement of sections of measures that make up the whole of the piece. In Mozart's time, piano sonatas were made up of two sections, the exposition and the recapitulation. In a one hundred measure composition it has been noted that Mozart divided the sections between the thirty-eighth and sixty-second measures. This is the closest approximation that can be made to the Golden Ratio within the confines of a one-hundred measure composition. Some scholars have debunked
this theory since further analysis of such compositions have shown that the Golden Ratio was not consistently applied within the subsections of the same compositions. Others state that this does not prove that he did not utilize the Golden Ratio, only that he did not apply it to all aspects of particular compositions. Whether he applied the Golden Ratio intentionally or used it intuitively is not known but studies seem to indicate the latter.
The Golden Ratio has also appeared in poetry in much the same way that it appears in music. The emphasis has been placed on time intervals. Some have even stated that the meaning of chosen words is less important than its rhythmic quality and the intervals between words and lines that serve to create the overall rhythm of a poem.
Probably the most compelling display of the Golden Ratio is in the many examples seen in nature. The Golden Ratio and the Fibonacci Sequence can be seen in objects from the human body to the growth pattern of a chambered nautilus. Examples of the Fibonacci Sequence can be seen in the growth pattern of a tree branch or the packing pattern of seeds on a flower. Ultimately, this aspect is what has earned the Golden Mean its representation as the Divine Proportion.
It is the prevalence of the Golden Ratio in nature that has influenced classic art and architecture. The great masters developed their skills by recreating things they observed in nature. In the earliest of cases, these artists and craftsmen probably had no knowledge of the math involved, only an acute awareness of this pattern repeated around them. It was the mathematicians that unlocked the secrets of the Golden Ratio. Their work has led to the understanding of the complex mathematical underpinnings hidden within the Golden Mean.
I now have a very clear understanding of why I was not taught how to create Golden Rectangle in that art class so many years ago. It would have required an understanding of some very complex math concepts and been beyond the scope of what that class was trying to teach. It is also quite likely that the instructor had no knowledge of the math involved in constructing a Golden Rectangle, only an awareness of it in much the same way as the masters did.
An interesting result has occurred due to my research, I now see the examples of the Golden Ratio everywhere. It is as if my eyes have been opened to something that existed all around me but to see. For that I am thankful.
This paper was written as an assignment for Ian Walton's Math G - Math for liberal Arts Students - at Mission College. If you use material please acknowledge it.
References
- Huntley, H.E. The Divine Proportion. New York: Dover, 1970.
- Runion, Garth E. The Golden Section. Palo Alto: Seymour, 1990.
- Vajda, S. Fibonacci & Lucas Numbers, and the Golden Section: Theory and Applications.Chichester: Ellis, 1989.
- Finch, Steven. The Golden Mean. Mathsoft. 6 Mar. 2001 http://www.mathsoft.com/asolve/constant/gold/gold.html.
- Weidman, K. The Golden Mean. 6 Mar. 2001 http://tony.ai/KW/golden.html
- Knott, Dr. Ron. The Golden Section in Art, Architecture, and Music. 6 Mar. 2001 http://www.ee.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibInArt.html
- May, Mike. Did Mozart use the Golden Section? Apr 1996. 17 Mar 2001 http://www.sigmaxi.org/amsci/issues/Sciobs96/Sciobs96-03MM.html
- Miller, Charles D., Heeren, Hornsby. Mathematical Ideas. New York: Addison, 2001.