Go to Math Dept Main Page | Go to Mission College Main Page

This paper was written as an assignment for Ian Walton's Math G -Math for liberal Arts Students - at Mission College. If you use material please acknowledge it.

To explore other such papers go to the Math G Projects Page.
 

It was a hot June afternoon in 1969, and I was sitting with my fellowclassmates through an unbearably long academic awards ceremony. I rememberbeing quite surprised to learn that my name had just been announced asthe winner of my Jr. High School‰s eighth grade "Outstanding MathematicsStudent" award. Although quite proud of my achievement, I remember experiencingan overwhelming feeling of bewilderment. I had assumed that one of theboys in my class would be the recipient of this award. As I glanced overat my mathematics teacher I could tell that he was quite pleased with hischoice. I remember his wink of approval, and the slight twinkle in hiseye. I felt sure then that it was not a mistake, he had actually chosenme for this award.

What I didn‰t know on that day was that the award would mark the endof my exposure to higher mathematics, rather than beginning it. My parentsfirmly believed (having grown up in the 1930‰s and ‰40‰s) that my roleas a female was to take high school courses that would help me land mea great job as a secretary. Possible college plans were reserved for theboys in my family. The boys, after all, would need to support a family.My future was determined. I was to work for a few years in the clericalprofession, and then find a nice man to settle down with. I would thenpresumably live happily ever after. After one year of freshman high schoolalgebra I switched to accounting and bookkeeping courses. By the time Ireached my senior year, due to my lack of exposure and my family‰s beliefsand attitudes, I had indeed concluded that I was "just no good at math."

With this belief system firmly intact, it has taken me over thirty yearsto finally find the courage to attempt a college mathematics course, forcedby my desire to attain a graduate degree. I have come to realize that mysuccess in mathematics classes is not necessarily influenced by my lackof ability, but rather by my lack of exposure to the subject area.

I have also come to realize that I am not alone. There has been an internationallyheld belief for the majority of the nineteenth and twentieth centuriesthat fundamentally women lack the biological make-up or necessary talentto succeed in higher mathematics. "First it was argued that their (women‰s)brains were too small, later that it would compromise their reproductivecapacities, still later that their hormones were not compatible with mathematicaldevelopment." (Henrion, 1997).

For centuries, women who exhibited a gift in the mathematical fieldhave faced many societal prejudices and obstacles in pursuing their mathematicalgoals. Before the early 20^th century women were banned fromformal entrance to universities and had to devise a variety of strategiesto further their education. Indeed, access to higher education has provento be one of the main barriers that women have faced not only in the fieldof mathematics, but in other subject areas as well.

A notable case is that of Sofia Kovalesvskaya, (1850-1891), a nativeof Russia whose ground-breaking work in mathematics made her male counterpartsreconsider their archaic notions of women‰s inferiority to men in the scientificarena. Sofia‰s work is considered one of the catalysts that allowed futurediscoveries in mathematics to occur. During her career, she published tenpapers in mathematics and mathematical physics. In 1888 she achieved hergreatest personal triumph by winning a competition sponsored by the FrenchAcademy of Science. Her winning entry titled "On the Rotation of a SolidBody about a Fixed Point" developed the theory for an unsymmetrical bodywhere the center of its mass is not on an axis in the body.

Sofia‰s mathematical accomplishments were not easily come by. In Russia,she was not allowed to study mathematics, and subsequently traveled toSwitzerland in order to try to gain entrance to a University there. However,young girls were not allowed to travel alone, so she entered into a marriageof convenience in order to travel to Switzerland to study mathematics.Sofia‰s goal was to seek the tutelage of Karl Weierstrass at the Universityof Berlin. Weierstrass was considered one of the most renowned mathematiciansof his time, and at first did not take Sofia seriously. After realizingher potential, he assisted her by privately tutoring her for four years.By the time she was finished, she had written three doctoral dissertationsin order to be awarded her Ph.D. (Henrion, 1997).

Another revolutionary female mathematician was Sophie Germain (1776-1831),who was also denied access to formal education. She studied mathematicson her own in her father‰s library, until she was caught studying her father‰smathematics books and reprimanded by her parents about it. She eventuallymade friends with several students at Ecole Polytechnique (a leading institutiondesigned to train mathematicians and scientists for the country of France,which women could not attend), and obtained their lecture notes. Subsequently,she submitted a memoir to the mathematician J. L. Lagrange under a malestudent‰s name. Lagrange saw talent in the work, sought out the author,and was quite surprised to find that it had been written by a woman. Sophie‰searly work began in number theory, but later shifted to applied mathematics.She became very curious about a phenomenon of "patterns produced on smallglass plates covered with sand and played, as though the plates were violins,by using a bow. The sand moved until it reached the nodes, and the arrayof patterns resulting from the "playing" of different notes caused greatexcitement among the Parisian polymaths. It was the first "scientific visualization"of two-dimensional harmonic motion. Napoleon authorized an extraordinaryprize for the best mathematical explanation of the phenomenon, and a contestwas announced." (Sophie Germain Website, 11/00). After three attempts atsolving the problem, Sophia finally won the prize on her third attemptin 1816.

These two women are representative of many women through out historywho have shown an aptitude for mathematics, and who were discouraged fromattempts to pursue this field of study. Eventually, however, by the late1800‰s and early 1900‰s women were gaining access to formal collegeeducation, and the mathematical field became more available for women.However, other obstacles stood in the way of women‰s complete acceptanceinto mathematics. "The ante continued to rise; no longer was a collegeeducation, or even a doctorate, sufficient credentials for membership inthe mathematical eliteáwomen were often formally or informally excludedfrom the inner circleáprogress for women in mathematics, even in the lastcentury was not necessarily linear."(Henrion, l997).

By the l970‰s the conversation had begun to change. Instead of centeringon access to mathematical education, women were focusing on attainmentof equity in the mathematical field. Membership and recognitionin the mathematical professional organizations still belonged mostly tomen. In addition, men dominated college professorships, with a few exceptions.As the women‰s cultural movement became increasingly more powerful in the1970‰s many questions were being raised. Why weren‰t women holding an equalnumber of professorships in mathematics across the country? Was it thatmen wouldn‰t give them the opportunity? Why weren‰t women equally representedin the national mathematical association‰s conferences?

Lenore Blum, a well known mathematician and one of the founders of TheMathematical Association of America‰s (MAA) Committee on the Participationof Women, spent some time researching the various mathematical societies‰conferences that occurred in 1971. She found that of the major mathematicalconferences scheduled that year, none of the conferences‰ invited speakerswere women. In addition, of the more than 300 ten minute talks, about fifteenwere given by women (5%). Additionally, many of the published programsfrom the mathematical conferences listed individuals‰ professional activitiesand achievements as well as job promotions and appointments. She foundthat of the thirty-one promotions listed, only three were female. As shewent down the list, she found that as the positions became less prestigious,the percentage of women increased. (A Brief History of the Associationof Women in Mathematics Website, accessed 11/25/00).

Violet H. Larney, in her article titled Female Mathematicians, WhereAre You? (1994) examined the hiring practices of women in higher mathematicaleducation during the same time period that Lenore Blum had investigated.Her study revealed some interesting facts. She defined a qualified femalemathematician as a female who possessed an earned doctorate in mathematics.She assumed age 25 was the minimum age at which a woman earned her Ph.D.,and that retirement was at age 65. "Then the female mathematicians qualifiedto hold academic appointments in 1970-71 would have earned their doctoratessome time during the preceding forty years. A few reference books and adesk calculator yield the figure of 816 as the total number of women whoreceived doctorates in mathematics from the academic year 1930-31 through1969-70áHence, the number of available women Ph.D.‰s is too small to averageeven one woman at each institutionáOne might safely conjecture that in1970 there was available only one female with a Ph.D. in mathematics forevery two degree-granting institutions in the United States."

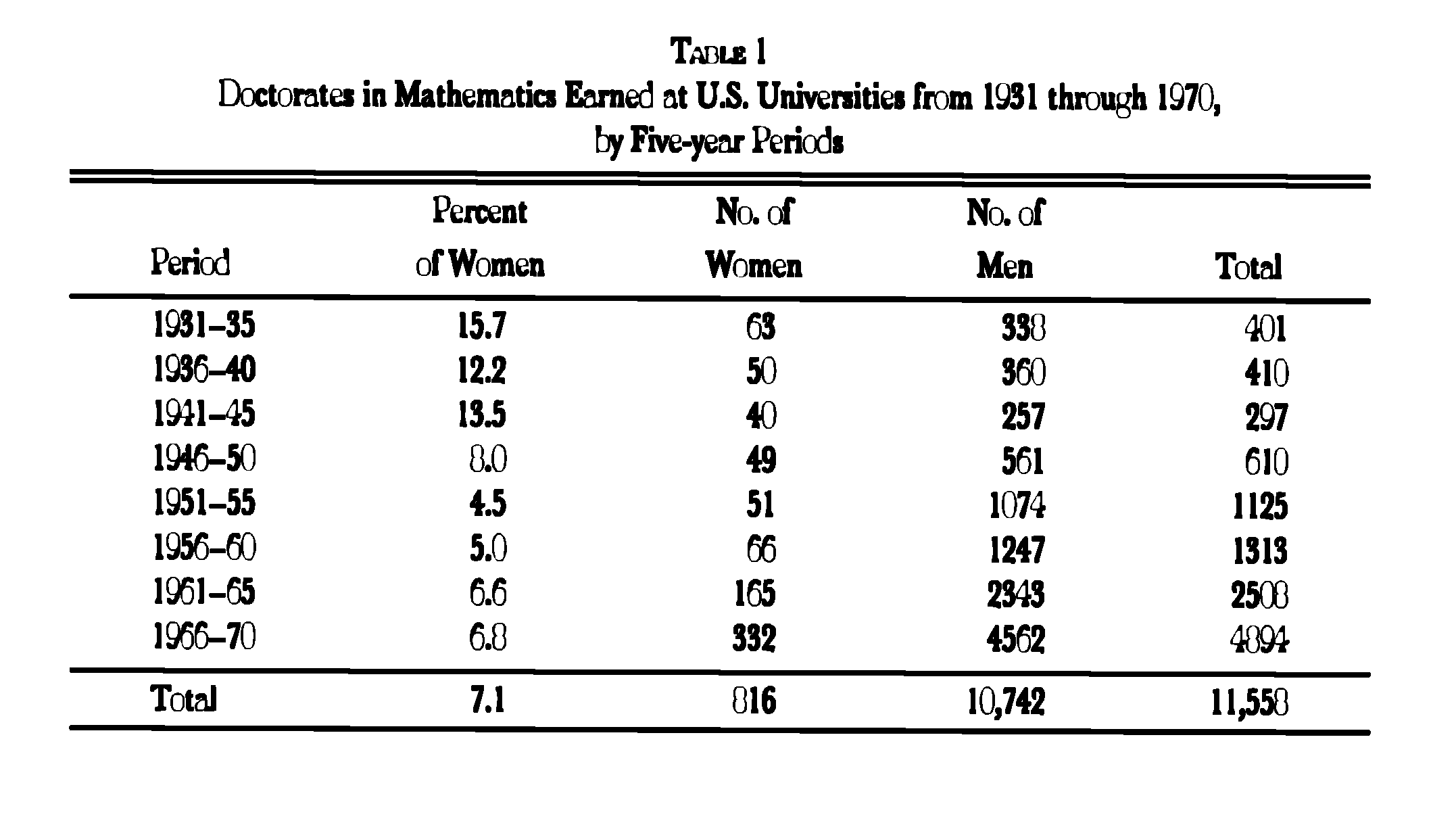
(Reprinted from A Century of Mathematics, John Ewing (Editor),page 282)
 
 

So, what has happened over the last thirty years? Has access and equityfor women in mathematics increased, and, are more women finding successin the field? Henrion (1997) reports that as of 1997:

• 44% of the math majors at the bachelor‰s degree level were women.
• At the top thirty-nine math institutions in the U.S., 37% of the bachelor‰s

• Women held 24% of the Ph.D.‰s., 17.4% of this 24% were from the top thirty-ninemath institutions in the U. S.

• Women make up 19% of full-time mathematics faculty across the U.S.
• Less than 10% of the 19% of full-time mathematics faculty that are womenare tenured.
• Women represent less than 5% of the mathematical faculty across the U.S.who hold positions in doctoral granting departments.

According to Henrion (1997), it is clear "that obstacles continue toexist to women‰s complete acceptance in mathematics. Though these obstaclesare rarely the blatant or formal barriers of the past, they continue toexist in more subtle forms, embedded in attitudes, beliefs, and expectationsabout women, mathematicians and mathematics."

The Mathematical Association of America‰s Committee on the Participationof Women agrees. In an article by Patricia Clark Kenschaft (1991), theysupport the argument that subtle barriers still exist. Ms. Kenschaft classifiesfive categories as the cultural reasons that too few women succeed at mathematics.These include:

• Societal Customs
• Family Customs
• Customs in our Educational System
• Customs Specific to Mathematics, and
• The Effects of these Customs on Individuals.

Studies have also shown that many girls become uninterested in mathematicsat the start of puberty. It is at this stage in their lives that the socialpressures of seeking popularity and the ability to "fit in" take precedenceover academic endeavors. In contrast, boys seem to thrive in an individuallycompetitive environment during this period, while girls thrive in a cooperativeenvironment. Several articles on the Weaving Gender Equity into MathReform Website (accessed 11/16/00) suggest solutions to losing girlsin mathematics at this stage in their development. The suggestions include:

• Teach mathematics in a cooperative learning style.
• Integrate mathematics into other curriculum areas that girls feel competentwith.
• Write about the thinking process in mathematics.
• A connection of math to real-life experiences helps to make it accessible.
• Alternative assessment to test taking improves elementary and middle schoolgirl‰s involvement in math classrooms.
• Girls do better in math when grouped together rather than focusing on individualizedinstruction.
• Girls don‰t realize as young teens which careers require math. It is importantto include this as part of mathematical education.
• Girls have lower expectations than boys do because they believethey lack ability. It is important to assist them in believing theyhave mathematical ability.

• Research shows that teachers give less attention and praise to girls inall subject areas. It is important for educators to become acutely awareof this and to continually examine and evaluate their behavior for biasin the classroom setting. (See attachment: Equity Checklist for theStandards-Based Classroom by Christina Perez).

• Responding to a son‰s inadequate performance in mathematics with "he mustwork harder," and responding to a daughter‰s performance with "I was nevergood at math either."
• Regarding the father as better at mathematics than the mother, and allowingthe father to be the authority on math.

An important book on how the use of mathematics is used in careers chosenby women is titled She Does Math(1995) by Marla Parker. Ms. Parkerexamines real-life problems contributed from women on the job in the manycareers that use mathematics. She includes women in careers such as EnvironmentalPsychology, Software Engineering, Archaeology, Computer Science, CivilEngineering, Astronaut Training, Real Estate Investment, and even FoodserviceManagement and Nutrition. Her reasoning is simple. "I created this bookfor two reasons: to motivate students to take math every year in high school,and to encourage high school and college students-especially women andminorities-to consider technical fields while planning their careersáHereis a collection of concrete answers to the question, "Why should I takemath?"

All in all, in retrospect, it must be said that opportunities availablefor women in the mathematical field have taken an incredible leap in thelast fifty years as compared to the last several centuries. Many associationsfor the support of women in mathematics have been created and creditedwith milestones and creative solutions in helping women to gain the accessand recognition they deserve in the field of mathematics. These includethe Association for Women in Mathematics, Women in Mathematics Education,and the International Organization for Women in Mathematics. Consideringthese milestones, it is quite likely that over the next century biasesregarding women and mathematics will disappear and equality will result,thereby giving women and other minorities equal access to careers (andthe high salaries that accompany those careers) in science, medicine andtechnology. As for me, I think I‰ll stick with the artsá

BOOKS

Ewing, John, H., Editor, A Century of Mathematics,Through the Eyes of the Monthly,

Washington, DC: Mathematical Association of America, 1994.

Henrion, Claudia, Women in Mathematics

Bloomington, Indiana: University Press, 1997.

Kenschaft, Patricia Clark, Winning Women into Mathematics,

United States: Mathematical Association of America, 1991

Nolan, Deborah, Women in Mathematics,

Berkeley, California: Mathematical Association of America,1997

Parker, Marla, She Does Math!

Washington, DC: Mathematical Association of America, 1995.

Perl, Teri, Women and Numbers,

San Carlos: World Wide Publishing/Tera, 1993.

Articles/Journals

Kenschaft, Patricia, Clark. Fifty-Five Cultural ReasonsWhy Too Few Women Win at Mathematics, The Mathematical Associationof America, 1991, pages 11-18.

Internet Resources

Girls Attitudes, Self-Expectations and Performancein Math by Michelle Maraffi

http://forum.swarthmore.edu/sarah/Discussion.Sessions/biblio.attitudes.html

Accessed: 11/16/00

Weaving Gender Equity into Math Reform

Three Articles on this website were used for reference:

Equity Checklist for the Standards-Based Classroom by Christina Perez

Facing Equity: Facing Ourselves by Fred Gross

Equity in Math Cooperative Groups by Hollee Freeman

http://www.terc.edu/wge/coopgroups.html

Accessed: 11/16/00

A Brief History of the Association for Women in Mathematics by LenoreBlum

http://www.awm-math.org/articles/notices/199107/blum/node2.html

Accessed: 11/25/00

Sophie Germain: Revolutionary Mathematician

http://www.sdsc.edu/ScienceWomen/germain.html

Accessed: 11/25/00

Sofia Kovalevskaya

http://www.scottlan.edu/lriddle/women/kova.htm

Accessed: 11/25/00

1. Introduction

1. My own experience in mathematics

1. As a woman graduating from high school in the early 1970‰s: Did my experiences(or lack thereof) in mathematics reflect the bias against women succeedingin mathematics, (the culture of the time) or was I really "just no goodat math"?

1. Body of Paper

1. What are women‰s experiences in math? What does the data/history show aboutwomen‰s involvement in mathematics?

1. There are historical beliefs that at the fundamental level women lack thebiological make-up and/or have insufficient talent to succeed in math.For some, this idea is still prevalent.
2. Historical lack of access to formal education for women.
3. Lack of access to mathematical ideas lest "women‰s health would becomeendangered" in intellectual pursuits. (Late 1800‰s).
4. Women historically have been actively discouraged to pursue math.
5. Women have lacked access to jobs in the mathematical fields.
6. Even when women were given access to formal education (late 1800‰s to early1900‰s) women were not given access to professional mathematical organizations.
7. In the 1960‰s and 1970‰s the focus changed from access to equity.
8. Even when the formal barriers started disappearing, women were not choosingto study math, thus locking themselves out of careers in science, medicineand technology (and the high salaries that accompanied those careers).
9. In the last two decades there has been a big effort to increase women‰sparticipation in math-related fields: (show some of those projects here).
10. Other relevant data:

1. 1997: 44% of math majors in US are women at Bachelor‰s degree level.
2. 37% of math majors (BS) at top 39 math institutions in US are women.
3. Beyond Bachelors: women currently 24% of PhD.‰s in math
4. Women represent 17.3% of Math PhD.‰s candidates at top 39 math institutions.
5. College math professors: Women represent:

 

 

-19% of full time faculty across US

-less than 10% of tenured professorships across the US

-less than 5% of doctoral granting departments across US

6. No women before 1990 were awarded prizes by the American Mathematical Society.
7. For minority women, these numbers are very, very low.

1. What are the educational issues involved in teaching and helping girlsgain access to mathematics in the elementary and middle schools?

1. Research shows that teachers give less attention and praise to girls inall subject areas.
2. Girls do better when grouped together.
3. Girls seem to not be making the connections to math and future careers.More education about careers related to mathematics is needed.
4. Girls have lower expectations than boys because they believe they lackability in math.
5. Parents and teachers attitudes and belief systems affect students. Researchshows that this begins as early as age four or five. Boys and girls aregiven different toys to play with.
6. Teachers need to continually examine and evaluate their behavior for biasin the classroom.
7. Girls are physically more mature at the 7^th to 10^thgrade levels. They did to focus more on their bodies and socializationskills than boys do at this crucial age.
8. Girls need cooperate learning styles, not independent thinking or competitiveprocesses to succeed in mathematics.
9. Integration of other subjects in elementary curriculum helps girls feelmore competent in math.
10. Math needs to be connected to real-life situations, so that skill transferencetakes place.
11. Alternate assessment (rather than a paper and pencil test) is shown toimprove girls involvement in mathematical classrooms.

1. Conclusion

1. What are the possible solutions?
2. What is currently being done to improve women‰s access to higher mathematics?
3. Who are the leaders in the move to improve access to women and mathematicsand what are they doing about it?

 

This paper was written as an assignment for Ian Walton's Math G -Math for liberal Arts Students - at Mission College. If you use material please acknowledge it.