Go to Math Dept Main Page | Go to Mission College Main Page

This paper was written as an assignment for Ian Walton's Math G -Math for liberal Arts Students - at Mission College. If you use material from this paper, please acknowledge it.

To explore other such papers go to the Math G Projects Page.
 

For centuries, mankind has been enthralled with the idea of time travel. In ancient Greece, much of their philosophy was based on the concept of eternity and the subject of time. All of the world‰s cultures revolve around time, but what is time? Is it possible to travel into the past or perhaps into the future? In this paper, I will discuss the physics of time, based on both Newtonian and Einsteinian physics, as well as consulting the opinions of today‰s scientists on the possibility of time travel. Today, time travel is used merely as fiction. Movies on the mysteries of time being harnessed have captivated their audiences. Scientists are striving to bring the concept of time from the world of fiction to reality. Several theories prove that it is a definite possibility, but first I will begin with simple formulas dealing with distance and time.

Though the study of time scientifically began during the lives of Galileo and Newton, not until Einstein was there a comprehensive explanation. He declared that time is only what a clock reads. This clock can be the rotation of a planet, a heartbeat, or sand falling through an hourglass. A grandfather clock, for example, follows the Newtonian Law, that states that the velocity of a body not subject to external forces remains constant. Plythagoras provided a formula that is applicable to right angled triangles in a flat Newtonian space, as seen below, with a, b, and c are the lengths of the sides of the triangle:

c^2=a^2+b^2.

There is always a relationship between speed, distance, and time. Velocity (or speed) equals the distance traveled divided by time. Or v= d/t . For example, if you traveled 10 miles in one hour, you would be going 10 miles per hour, as shown below:

Here is another example how speed can stay the same even though time and distance may change.

Sounds easy enough so far, further exploration on the matter provides some interesting results. They begin by being predictable, but as the velocity picks up, you will notice that Newtonian laws begin to fade.

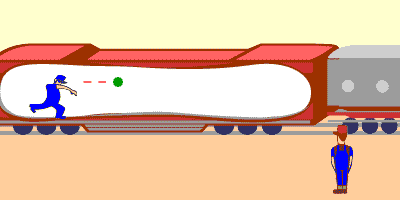
Let‰s begin by adding velocities, place yourself on a train going at 50 mph. You throw a ball in the direction that the train is moving. Relative to you and the train, the ball is going 20 mph. If someone was standing near the tracks watching you throw the ball (assuming they could see you in the train car, pretend it‰s glass), how fast is the ball moving?

The answer would be 70 mph, adding both the 50 mph of the train, and the 20 mph of the ball leaving your hand. Right now, things are making sense. But will it still make sense if the train begins moving at the speed of light (again assuming that Amtrak could go that fast)?

In 1887, two American scientists performed an experiment. The results showed that the speed of light was independent of motion. Light always traveled at the same speed (which is 186,000 miles per second), whether the source of light or the observer was moving. There was also an indication that the speed of light was constant too, something that fascinated Einstein. A 19^th century mathematician and physicist named James Clerk Maxwell discovered equations that described the nature of electricity, magnetism, and most importantly (for this term paper), light. He presented a derivation that light consists of transverse undulations of the same medium, which is the cause of electric and magnetic phenomena. These equations are far too complex for me to simply place on the paper and explain. Needless to say, his equations helped Einstein greatly on his study of the speed of light.

Going further with the train theory, it suddenly picks up speed and begins to move at 93,000 mps (miles per second). To give an idea at the amazing horsepower of this train, going at this rate, it would have to circle the world (which is approximately 24,000 miles around) four times per second. This dangerous speed has only been attempted by few on our local freeways. You are standing in the speeding train, and there is still an observer watching. This time, instead of throwing a ball, you turn on a flashlight. Relative to the observer standing by the tracks, how fast would the light travel?

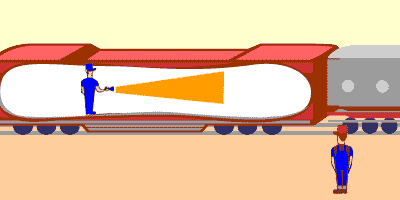
To the observer, the light would be travelling at 186,000 mps. It‰s constant speed. This may not seem to make much sense but it has been proven through many experiments.

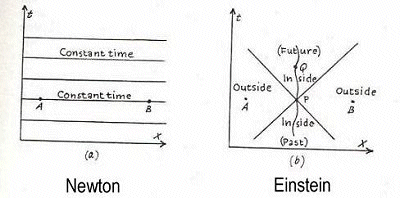
Returning to Newton‰s theories, one of his contributions to scientific discovery was the definition of how motion changes with time. He showed the force causing apples to fall is the same force that is behind the planetary motions and produces tides. However, Newton was still baffled by the fact that gravity seemed to operate instantaneously at a distance, and was unable to describe it. Einstein‰s general theory of relativity changed gravity from a vague ëforce‰ to the movement of matter along the shortest space in a curved space time. Newton believed that both time and space were absolute. They were a fixed, infinite, unmoving metric by which absolute motions could be measured. He also believed that the universe was controlled by a single absolute time that could be symbolized as an imaginary clock floating in space. Einstein changed all this by proving that time was relative.

Now we move on to our last theoretical experiment on the train. We know how fast the light appeared to be going for the observer, how fast does it seem to be travelling for you on the train? Again, the speed of light remains constant, and you view it going at the same speed as the observer saw it, which was 186,000 mps. This presents a strange paradox. It seems unreasonable that light should always travel at the same speed no matter how fast its source is moving. The v= d/t formula worked well in the first scenario, but it did not work for the second scenario with the flashlight instead of the ball. The ëv‰ in the equation has to be 186,000 mps since the problem was dealing with the speed of light. These experiments lead to one conclusion. Time (and perhaps even distance) is not the same for all observers.

The idea that time and distance are not fixed goes directly against our common sense. In the second and third train experiments, the speed of light is going at the same pace for you as it is for the observer because time (judging by your watch) ticked at a slower rate than that of your friend looking at you by the tracks. Distance is also altered, for example, a one foot ruler on the train would have appeared much smaller to the observer. Yet still, for you riding in the train, time wouldn‰t be moving slower, and the ruler wouldn‰t be shorter. All would look normal to you.

Let‰s take a closer look at Einstein‰s theory of relativity, beginning with the formula discovered by Pythagoras that was stated before: c^2=a^2+b^2. According to Einstein‰s theory of Relativity, neither time, length, or even mass remain constant additive quantities when approaching the speed of light, which is c. Our ideas of time and space come from mankind being too used to living in a three dimensional universe. Einstein showed that this was not true, and that the laws of Newton would have to give in to the Lorentz factor: L_f=(1-v^2/c^2)^1/2.

Einstein and Newton obviously viewed our universe very differently, as shown by the diagrams below.

A dramatic way of illustrating this paradox is to have a set of identical twins participate in an experiment in which one twin leaves the earth in a fast rocket which travels at near the speed of light to the nearest star and back again. The time for this round trip measured by the twin on earth is several years, but for the twin in the rocket this travel time may be made as short as he pleases by closely approaching the speed of light. In other words, time for the twin in the rocket travels slower than time for the twin on the earth. The traveling twin will return to earth several years younger than his stay at home sibling, having only experienced a short travel duration against several years duration on earth. With sufficient resources to achieve near-to-light rocket speeds anyone may travel indefinitely far into the future in this way. People that live in higher altitudes age 10 to the minus 12^th seconds slower than their counterparts in a lower altitude solely on the basis of the increased speed at high altitudes from the earth‰s rotation. Let‰s take a look at a log kept by A(in the rocket) and B(left on earth).

Using a specific example, suppose that twin A travels to a nearby star 10 light years away at a uniform speed of 0.9c, i.e. 90% of the speed of light. He then returns immediately to earth at the same speed. We will ignore periods of speeding up and slowing down. All the while twin B remains on earth with his own clock observing A, as he leaves and then returns. Using the Lorentz factor mentioned above, this shows that both twins will observe the other‰s clock to run 2.3 times too slow. Now at the speed A is going (at 90% the speed of light) he will cover the distance of 10 light years in 11.1 earth years as measured by B on his own clock. But because of time dilation this event will be recorded as only 4.84 years on A‰s rocket clock. To summarize the whole trip, the following table shows the earth clock and the rocket clock for both the outward and return journey:

  It is possible to use the round trip experiment to illustrate another remarkable conclusion of the special theory of relativity. A is traveling at 0.9c relative to the earth but covers the distance from the earth to the nearby star in only 4.84 rocket years. It follows that this distance must appear to A to be only 0.9 x4.84=4.36 light years, rather than 10 light years as measured by B. The spatial distance, therefore, has shrunk by the same factor as the time interval has stretched. The factor again being the Lorentz formula as mentioned above.

Einstein‰s theory of Relativity can also be explained in simpler terms. This theory is actually split up into two. The special theory of relativity (discovered in 1905) and the general theory of relativity (1915). The special theory gives a unified account of the laws of mechanics and electromagnetism. As mentioned before, Einstein didn‰t believe the concepts of absolute space and time. He accepted that the laws of nature are the same for all observers in uniform relative motion and that the speed of light is the same for all observers. The experiment of the clocks moving slower in the train is the phenomenon of time dilation. The mathematical formula for the special theory of relativity is based on the idea that an event is specified by four coordinates: three spatial coordinates and one time coordinate. This is where the fourth dimension term comes from. These coordinates define a four dimensional space and the motion of a particle can be described by a curve in this space. The special theory of relativity centers around relative motion between non-accelerated frames of reference. Distance that we travel is often related to another object. For example, if we wanted to know our speed and direction on earth there would be no problem. If a car travels 60 miles from one place to another in one hour it has traveled at the speed of 60 mph. We could even measure the distance if we had to prove it. So there is something definite to go by, the ground by which we have traveled. And airplanes use air speed indicators to measure their speed. So as long as there is some familiar body in view, direction and rate of speed can be measured.

Beyond sight of the earth, moon, planets and sun, little else remains. Let us say that while you are in your rocket deep in space you see a meteoroid pass by your window, would that mean it was traveling faster than you? You might conclude yes. But are you sure? Might it be, instead, that you are stopped and it was passing you? Or was the meteoroid the one that was stopped and were you actually going backward? Or were you both going backward, but your backward rate was faster than that of the meteoroid? In fact, how would you really know what was backward or forward in outer space. You can see the complications of trying to determine motion in space. There must be some familiar body with which a traveling object can be related. Hence, all motion in space is relative, that is, faster, slower, forward or backward in comparison to something else. This is the basis of the theory of relativity.

The general theory deals with general relative motion between accelerated frames of reference . Most of the tests of this theory have been through observations in astronomy. This theory explains the bending of light or other electromagnetic radiation in the presence of large bodies. Since this has little to do with the time subject, the general theory will be glossed over.

It was the sudden boom of science fiction novels written in the 1980‰s that sparked a huge interest in the investigation of time travel. Scientists discovered the phenomenon of the wormhole in space. Wormholes are tunnels in the fabric of space and time predicted by Einstein‰s equations. Kip Thorne, an astrophysicist, quotes: "Our universe- it‰s three dimensional, but we can pretend it‰s two-dimensional so it‰s like a sheet of paper- and we live in Pasadena over here and London is over there and it‰s thousands of miles from Pasadena to London. This universe is curved up so that through hyperspace, the distance from Pasadena to London is only a few feet and there is this pipe, this little wormhole that will lead us from Pasadena to London across that very short distance, and it‰s like looking through a crystal ball. You see a distorted picture of what is going on at the other mouth of the wormhole which may be in another galaxy or it may be near the star Vega or it may be in London." But could these wormholes really be a reality? With the possibility of these wormholes, time travel seemed feasible. At least in theory.

The twin paradox as mentioned above is also connected to the wormhole theory. By taking advantage of the twin‰s paradox they could send one mouth of a wormhole on a voyage into outer space. As the wormhole mouth approaches the speed of light, time slows down relative to the wormhole mouth that is still on earth. Similar to the twin‰s paradox, less time has passed for the outer space wormhole side, than the other side that is at earth. The wormhole is now a tunnel with each mouth located in a different time. Thorne remarks: "If I now go into this wormhole mouth today, I will come out of that mouth yesterday." Meaning that he would go into the wormhole on earth and arrive in the past out of the wormhole on the other side.

Again, in theory, the wormhole phenomenon makes time travel look almost easy. However, where would one find wormholes? Scientist John Wheeler provided an answer, comparing space and time to waves on the ocean. Waves don‰t show up when one is miles above the sea, it looks flat. As one gets closer to the surface, they can see the waves breaking and the sea foam. As said by Wheeler, "I see no way to escape the conclusion that similar foam-like structure is developing in space and time." Wheeler believes that the space between atoms is filled with bubbles, and this ëquantum foam‰ (as he dubbed it) gives rise to extremely tiny wormholes. If quantum foam exists, there might be a way to enlarge these little wormholes.

There are two arguments, basically that you can go back in time using wormholes and the other that something would prevent you from going back in time in a wormhole. Here is a list of the reasons why some think that it is impossible to do any time travel using a wormhole.

1. Wormholes live for a very short time so some way would have to be devised to keep it open.
2. How come there are no people from the future around? (as if they would want to come back to this time period.)
3. You can‰t go back in time until a time machine is invented.
4. The wormhole will explode when it gets back to earth. (That is what Stephen Hawking and Kip Thorne believe).

Currently both Stephen Hawking and Kip Thorne feel that you cannot make a time machine and go backward in time, ever. But until we have those full laws of quantum mechanics we just have to leave it as a possibility that remains only a possibility.

Researchers are still proposing ways in which backward and forward time machines can be built that do not seem to violate any known laws of physics.

The laws of physics merely tell us what is possible, not what is practical for humans at this point in time. The physics of time travel are still mainly theoretical. While all physicists today admit that time travel to the future is possible, many still believe time travel to the past will never be easily attainable. Don't be quick to believe anyone telling you that humans will never have efficient technology for backward and forward time travel. Accurately predicting future technology is nearly impossible, and history is filled with underestimates of technology. In conclusion I‰d like to quote Stephen Hawking who made this remark "I wouldn‰t take a bet against the existence of time machines, my opponent might have seen the future and knows the answer."

The following quotes show evidence that man can sometimes misjudge what lies ahead in the future:

"Heavier-than-air flying machines are impossible." (Lord Kelvin, president, Royal Society, 1895)

"I think there is a world market for maybe five computers." (Thomas Watson, chairman of IBM, 1943)

"There is no reason for any individual to have a computer in their home." (Ken Olsen, president, chairman and founder of Digital Equipment Corp., 1977)

"The telephone has too many shortcomings to be seriously considered as a means of communication. The device is inherently of no value to us." (Western Union internal memo, 1876)

"Airplanes are interesting toys but of no military value." (Marshal Ferdinand Foch, French commander of Allied forces during the closing months of World War I, 1918)

"The wireless music box has no imaginable commercial value. Who would pay for a message sent to nobody in particular?" (David Sarnoff's associates, in response to his urgings for investment in radio in the 1920's)

"Professor Goddard does not know the relation between action and reaction and the need to have something better than a vacuum against which to react. He seems to lack the basic knowledge ladled out daily in high schools." (New York Times editorial about Robert Goddard's revolutionary rocket work, 1921)

"Who wants to hear actors talk?" (Harry M. Warner, Warner Brothers, 1927)

"Everything that can be invented has been invented." (Charles H. Duell, commissioner, US Office Patents, 1899)

Not all of these words were used in my report, but you might find it helpful anyway.

absolute space: Newton's conception of the three-dimensional space in which we live as having a notion of absolute rest, and as having the property that the lengths of objects are independent of the motion of the reference frame in which they are measured.

absolute time: Newton's conception of time as being universal, with a unique, universally agreed upon notion of simultaneity of events and a unique, universally agreed upon time interval between any two events.

chronology protection conjecture: Stephen Hawking's conjecture that the laws of physics do not allow time machines.

curvature of space or spacetime: The property of space or spacetime that makes it violate Euclid's or Minkowski's notions of geometry; that is, the property that enables straight lines that are initially parallel to cross.

event: A point in spacetime; that is, a location in space at a specific moment of time. Alternatively something that happens at a point in spacetime, for example, the explosion of a firecracker.

exotic material: Material that has a negative average energy density, as measured by someone moving through it at nearly the speed of light.

field: Something that is distributed continuously and smoothly in space. Examples are the electric field, the magnetic field, the curvature of spacetime, and a gravitational wave.

freely falling object: An object on which no forces act except gravity.

general relativity: Einstein's laws of physics in which gravity is described by a curvature of spacetime.

geodesic: A straight line in a curved space or curved spacetime. On the Earth's surface the geodesics are the great circles.

gravitational time dilation: The slowing of the flow of time near a gravitating body.

gravitational wave: A ripple of spacetime curvature that travels with the speed of light. hyperspace: A fictitious flat space in which one imagines pieces of our Universe's curved space as embedded.

mouth: An entrance to a wormhole. There is a mouth at each of the two ends of the wormhole.

Newtonian laws of physics: The laws of physics, built on Newton's conception of space and time as absolute, which were the centerpiece of 19th-century thinking about the Universe.

perturbation: A small distortion (from its normal shape) of an object or of the spacetime curvature around an object.

Planck-Wheeler length: The Planck-Wheeler length (1.62 x 10-33 centimeters) is the length scale below which space as we know it ceases to exist and becomes quantum foam.

principle of absoluteness of the speed of light: Einstein's principle that the speed of light is a universal constant, the same in all directions and the same in every inertial reference frame in the absence of gravity.

quantum foam: A probabilistic foamlike structure of space that probably makes up the cores of singularities, and that probably occurs in ordinary space on scales of the Planck-Wheeler length and less.

quantum gravity: The laws of physics that are obtained by merging ("marrying") general relativity with quantum mechanics.

quantum mechanics: The laws of physics that govern the realm of the small (atoms, molecules, electrons, protons), and that also underlie the realm of the large, but rarely show themselves there.

reference frame: A (possibly imaginary) laboratory for making physical measurements, which moves through the Universe in some particular manner.

relative: Dependent on one's reference frame; different, as measured in one frame which moves through the Universe in one manner, than as measured in another frame which moves in another manner.

simultaneity breakdown: The fact that events which are simultaneous as measured in one reference frame are not simultaneous as measured in another frame that moves relative to the first.

singularity: A region of spacetime where spacetime curvature becomes so strong that the general relativistic laws break down and the laws of quantum gravity take over. If one tries to describe a singularity using general relativity alone, one finds (incorrectly) that tidal gravity and spacetime curvature are infinitely strong there. Quantum gravity probably replaces these infinities by quantum foam.

spacetime: The four-dimensional "fabric" that results when space and time are unified.

spacetime curvature: The property of spacetime that causes freely falling particles that are initially moving along parallel world lines to subsequently move together or apart. Spacetime curvature and tidal gravity are different names for the same thing.

spacetime diagram: A diagram with time plotted upward and space plotted horizontally.

special relativity: Einstein's laws of physics in the absence of gravity.

tidal gravity: Gravitational accelerations that squeeze objects along some directions and stretch them along others. Tidal gravity produced by the moon and sun is responsible for the tides on the Earth's oceans.

time machine: A device for traveling backward in time. In physicists' jargon, a "closed timelike curve."

warpage of spacetime: Same as curvature of spacetime.

world line: The path of an object through spacetime or through a spacetime diagram.

wormhole: A "handle" in the topology of space, connecting two widely separated locations in our Universe.

Time and the Physical World, Richard Schlegel. Michigan State University Press, MI 1961

Space and Time in the Modern Universe, P.C.W. Davies. Cambridge University Press, NY 1977

Beyond Numeracy-Ruminations of a Numbers Man, John Allen Paulos. Alfred A. Knopf, Inc.

NY 1977

Timewarps, John Gribbin. Dell Publishing Co., NY 1979

http://pbs.org/wgbh/nova/time