Go to Math Dept Main Page | Go to Mission College Main Page

This paper was written as an assignment for Ian Walton's Math G -Math for liberal Arts Students - at Mission College.

To explore other such papers go to the Math G Projects Page.
 

Math G_Lisa Corbett

Ian Walton_December 6, 1999

Albert Einstein once said in a letter to Max Born: "You believein a God who plays dice, and I in complete law and order."Chaos gives way to order, which then gives rise to new forms ofchaos. Deterministic disorder.

Ancient Theory

In ancient times, people thought of chaos as something immenseand creative. Some thought of our beginnings as a state of chaos,or nothingness, from which beings and things came from. A Chinesestory says that a ray of light, yin, jumps out of chaos and buildsthe sky while the heavy dimness, yang, forms the earth. Yin andyang then create everything else. The principles of yin and yangare said to retain the qualities of the chaos they came from.The story finally says that too much yin or yang will bring chaosback.

The Babylonians have a story of chaos that has a god symbolizingthe "boundless stretches of primordial formlessness",of representing the intangibility and imperceptibility that existsin chaotic confusion. They believed that new forms came out fromchaos and began to give structure to the universe.

Even in Christianity, there are stories related to chaos. In Psalm74:13-14, it is related that God (who is order) is compelled to"break the heads of the dragons on the waters" and "crushthe heads of Leviathan." This follows the notion of creationthat emphasizes the struggle of the deity against the powers ofchaos. The Biblical universe starts "without form, and void"until God creates, or orders, it. It would take modern sciencethousands of years to show a different face of chaos, a kind ofvirtual order.

Until recently, chaos has had two definitions in the dictionary:the disordered formless matter that existed before the ordereduniverse; and complete disorder or utter confusion. But recently,referring to a scientific conference held in 1986, yet anotherdefinition of chaos was proposed: stochastic (random) behavioroccurring in a deterministic system (a system ruled by exact andunbreakable law). Deterministic systems that maintain themselvesby oscillations, iterations, feedback or limited cycles are vulnerableto chaos and face an unpredictable fate if pushed beyond criticalboundaries.

A seemingly orderly, repetitive and predictable motion becomesa chaotic episode and has mystified scientists and mathematiciansfor hundreds of years. What was thought to be simple becomes complicated.A complicated action becomes simple. And even the simplest equationscan generate motion so complex, so sensitive to measurement thatthis motion appears to be random. Randomness in nature occursnaturally and is to be expected. Reductionism (NewtonÌscause-and-effect determinism) imagines nature as equally capableof being assembled and disassembled. And reductive scientistsbelieve the most complex systems are made up of many differentelements that have been combined by nature in innumerable ways.Chaotic patterns are somewhat unpredictable. They are so complexthat scientists in the past could not track them.

One of the fundamental characteristics of a chaotic physical systemis its sensitivity to initial conditions. Sensitivity means thatif two identical mechanical systems are started at initial conditionsx and x+ E, where E is a very small quantity, their dynamicalstates will diverge from each other very quickly in phase space,their separation increasing exponentially on the average. Themotion of a swinging pendulum is an example of this. A chaoticpendulum originating at two nearby points will have trajectoriesthat diverge markedly in less than one forcing period.

In the nineteenth century, scientists wondered why they couldnÌtinvert a perpetual motion machine. Whenever they ran a machine,some of the energy fed into it turned into a form that they couldnot recover and use again. The energy had become disorganized,chaotic.

Chaos seems to have laws of its own. Irregularities in naturehave mystified scientists for years, and chaos has brought themto the surface of the scientific world. Chemists, biologists,physicists and mathematicians have all been looking for a connectionbetween the different kinds of irregularities.

One physicist said "Relativity eliminated the Newtonian illusionof absolute space and time; quantum theory eliminated the Newtoniandream of a controllable measurement process; and chaos eliminatesthe Laplacian fantasy of deterministic predictability."

The relatively new science of chaos has its own language. Wordslike fractals, bifurcations, intermittencies, periodicities, folded-toweldiffeomorphisms and smooth noodle maps are but a few examplesof the new vocabulary. There are special techniques of using computersto study chaotic behavior. Some physicists believe that chaosis a science of process rather than state, of becoming ratherthan being. There are some that believe the fate of the universedepends on the distribution of matter within it.

Chaos is all around us. It effects all phases of science, medicine,weather and even the topography of the Earth. It plays a partin just about every aspect of our world. The reversals of EarthÌsmagnetic fields, the collision of atoms of gas, irregular heartbeats,even the dripping of a faucet and the bouncing of a billiard ballall have chaotic properties.

Experiments in Chaos

Chaos has been around for thousands of years, but the first truescientific experiments in chaos theory were not performed until1960 by a meteorologist named Edward Lorenz. He input twelve mathematicalequations into a computer program used to predict what the weathermight be.

One day, he wanted to repeat a particular sequence. In order tosave time, he started in the middle of the sequence instead ofthe beginning. He entered the figures into the computer, and leftthe room to let it run. During the next hour, the sequence actuallychanged from what it had been previously. He learned purely byaccident that even a small change in the initial conditions drasticallychanges the long-term behavior of a system. His chaos theory showsthat it is sensitive dependant on initial conditions: where andat what point something starts and where it is at any given pointwill decide where it will go next. Linearity is a structured,predictable concept. Twice the force equals twice the distancean object will travel. Non-linearity shows that a small forcecan make an unpredictable reaction; thus, the concept of chaos.

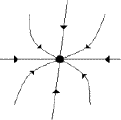
A dynamical system is loosely defined as anything that has motion.There are many different types of motion that can be exhibitedby a dynamical system. The simplest is fixed point behavior. Anexample of this behavior is the movement of a pendulum when frictionand gravity bring the system to a halt. Most fixed points canbe compared to a ball that rolls downward until it sits on a flatspot and has no momentum to carry it further.

The next simplest type of motion is known as a limit cycle orperiodic motion. This motion involves movement that repeats itselfover and over. A planet in our solar system orbiting the Earthhas a periodic motion.

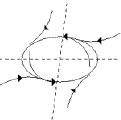
Amore complicated form of motion is found in a quasiperiodic system.These systems are similar to periodic systems, but they do notquite repeat themselves. The moon orbits Earth, which orbits thesun, which, in turn, orbits the galactic center, and so on. Inorder for the combined motion of the moon and Earth to be trulyperiodic, they must at some future point return to some previouslyoccupied state. But for this to happen, all of the individualmotions must resonate, which means that there must exist a lengthof time that will evenly divide all of the frequencies.

Fixed Point Limit CycleQuasiperiodic

One helpful element of analysis in chaos theory involves bifurcationdiagrams. In dynamics, a change in the number of solutions toa differential equation as a parameter is called a bifurcation.These diagrams can provide a summary of the essential dynamicsinvolved. The dynamics may also be viewed more globally over arange of parameter values. This allows for simultaneous comparisonof periodic and chaotic behavior. An experiment involving thecycle and pattern of a pendulum is an example having bifurcationdiagrams. For some values of the parameters, a pendulum will haveonly one long-term motion. But for slightly different values,two or more motions may be possible. If several of them are stable,the actual behavior can depend on initial conditions.

If the pendulum is lightly driven and the motion is periodic withthe same period as the drive frequency, then the velocity hasone value at a given time during the drive cycle. If the parameteris increased sufficiently, further components of longer periodare added to the motion, and there will now be more than one valueat the given phase. This system had undergone a bifurcation.

Chaos and Ecology

Some ecologists use mathematical models to study species and theirdevelopment. They treat populations as dynamical systems. In mathematics,regular equations can produce irregular behavior. The equationsapplied to population biology were simple counterparts of themodels used by physicists for their pieces of the universe. Physicistscan look at a certain system and choose the appropriate equationsto solve the problem at hand.

But the life sciences are very complex. A biologist can neversimply choose the proper equations and solve the problem by justthinking about an animal population. He must first gather dataand try to find the equations that produced similar output. Thereare questions that formulas must be applied to. Questions suchas "what happens when you put one thousand fish in a pondwith a limited food supply?" and "what happens if youadd fifty sharks that like to eat two fish per day?" arecommon ones to an ecologist. What happens to a virus that killsand spreads at a certain rate depending on population density?Scientists applied mathematical formulas to these questions thatsometimes worked to solve the issue. Population biology learnedquite a bit about the history of life, how predators interactwith their prey and how a change in the population density ofa country can affect the spread of disease.

If a certain mathematical model went ahead or died out, ecologistscould guess something about the circumstances in which a realpopulation or epidemic would do the same. Differential equationsdescribe processes that change smoothly over time, but differentialequations are hard to compute. Simpler equations, "differenceequations", can be used for processes that jump from stateto state. Many animal populations do what they do in one-yearintervals. Changes during the short time of a one-year span arevery often more important than changes in a longer time-span.Many insects stick to a single breeding season, so their generationsdo not overlap as humans do. An ecologist might need only correspondingfigures from the previous or current year to make predictionsfor

the coming season. A year-by-year model can produce only a thinlayer of information about a systemÌs minute details. However,in many applications, this layer provides enough information forthe scientist to complete his research successfully.

The mathematics of ecology is actually quite simple. Basic functionequations are common elements. Following a population throughtime is a matter of taking a starting figure and applying thesame function over and over again. The whole history of the populationbecomes available through this process of functional iteration.Another example of studying population growth is to use a linearfunction that would show a rise in population a certain percentageeach year. A function like this would continuously show a growthevery year. But in the real world, that is not always the case.

Ecological mathematicians now realize that they must find a functionthat more accurately matches the realities of life. Hunger andcompetition in the animal kingdom are examples of the harsh realitiesthat affect the population of these animals. A more realisticfunction needs to contain an extra term that restrains growthwhen the population becomes large. The most natural function tochoose would rise steeply when the population is small, reducegrowth to near zero at intermediate values, and move downwardwhen the population is very large. By repeating the process, anecologist can watch a population settle into its long- term behavior.

In the 1950Ìs, scientists were studying the variationsof this logistics difference equation. It contained variablesrepresenting the reproductive rate, the natural death rate andthe additional death rate from starvation or predation among thespecies. They showed that the population would rise at a certainspeed until it reached a certain level of equilibrium. But thescientists wanted to know how the changing parameters in the equation(representing growth rate) would affect the ultimate destiny ofa changing population. The most obvious answer was that a lowerparameter would cause a population to end up at a lower level.A higher parameter would lead to a higher steady state. This assumptionwas correct for some parameters, but not all of them. Occasionally,researchers tried parameters that were even higher, and when theydid, they witnessed chaos.

The flow of numbers began to misbehave. They continued to grow,but did not converge to a steady level, as was expected. Withpopulations bouncing back and forth, ecologists assumed that itwas oscillating around some underlying equilibrium. The equilibriumwas the important thing. It did not occur to the ecologists thatthere might be no equilibrium. During the 1960Ìs, textbooksand reference books did not even acknowledge that chaotic behaviorcould be expected. There was presented a standard sense of possibilities.Populations could remain constant or fluctuate around a presumedequilibrium point. The researchers knew that, in real life, populationsdo behave erratically.

But from a scientific point of view, they assumed that erraticbehavior had nothing to do with the sort of mathematical modelsthey were describing. And if models started to betray their makersÌknowledge of the real populationÌs behavior, some missingfeature could always explain the discrepancy. They could and didassume simply that numbers on the calculator were not accurate.The stable solutions were the interesting ones. Order was itsown reward. Finding appropriate equations and working out thecomputations was not an easy job. Ecologists did not want to wastetime on a line of work that was going awry, producing no stability.They knew that their equations were oversimplified versions ofthe real phenomena. The point was to model regularity. Why goto all the trouble just to see chaos?

Chaos and Medicine

One application of chaos in medicine is used to study problemswith the heart. An irregular heartbeat, known as arrhythmia, cansometimes be fatal. The heart beats at irregular intervals andsometimes with varying intensity instead of the normal, regular(predictable?) heartbeat. A fibrillating heart is never all contractedor all relaxed. The electrical wave that travels throughout theheart is broken up.

It has been established in the medical field that these arrhythmiasare manifestations of chaos. They follow fractal laws. They lackthe order that should be present.

A doctor listening to a heartbeat hears the sounds of fluid whooshingagainst fluid, against solid, and solid against solid. Blood flowing,valves opening and closing and muscles contracting are all partof the inner workings of the heart. The muscle contractions themselvesdepend on a complex three-dimensional wave of electrical activity.Modeling any one piece of the heartÌs behavior would straina supercomputer; modeling the whole interwoven cycle would beimpossible.

Hospitals today rely upon professionals to interpret a patientÌsEEG, with respect to the "randomness" of the heartbeat,and offer a solution that will help restore the "predictableregularity" to the heartbeat. Irregular heartbeats have beencategorized and investigated. There are dozens of names for thevarious irregular rhythms associated with the heart. Doctors usethis information for diagnosis of heart problems. By using thetools of chaos, researchers have now discovered that traditionalcardiology has been making the wrong generalizations about irregularheartbeats, inadvertently using superficial classifications toobscure deep causes.

At this point in time, training for cardiologists does not includemuch mathematics. But now that research has shown that nonlinearmathematics can help to understand these rhythms and their orderings,future cardiologists-in-training will most definitely use moremathematics to solve medical problems.

Chaos and Gasses

The motion of gaseous substance is chaotic. In an experiment,one can control the motion of the gas with the use of heat andcold. Heated gas inside of a box will rise up one side and seemto "roll" to the other side and lower in the box asit cools, effecting a "rolling pattern". But natureis not so predictable. Heated gasses will roll around in one direction,but will stop and reverse directions at random. This "randomness"is repeated in a seemingly "random" pattern; but atunpredictable speeds and unpredictable times.

Chaos and Weather

There are many variables that go into a weather forecasting equation.Air temperature, air pressure, wind velocity, wind direction andhumidity are a few of these variables. Too many elements can seemto make an outcome unpredictable. We might think that physicallaws govern the changes in the weather from one moment to thenext. These laws would seemingly make prediction possible. Butnature is full of "unexplainable" phenomena and many"unpredictable" changes, making it difficult to accuratelypredict the weather more than a few days in advance.

Yet, we are able to predict the high and low tides quite accuratelyfor an entire year. In predicting the tides, consider that theocean and the atmosphere are both large fluid masses that almostcompletely envelop the earth. They have similar physical laws.They both have fields of motion that tend to be drawn out by internalprocesses; yet, are driven by varying external influences. Theyare two components of a larger dynamical system, since each exertsa considerable influence on the other at the surface where theycome into contact. The winds produce most of the oceanÌswaves. Evaporation from the ocean supplies the atmosphere withmost of the moisture that eventually condenses and falls backinto the ocean as rain or snow. The heat from the sun and gravitationalpull of the sun and moon are also external forces that drive theposition of the tides.

A regular response to these forces is the height of the tides.An irregular response might be an unusually high wave caused byexcessive winds.

Weather variations are often thought of as not periodic. But theyhave periodic components (the cooling and warming during seasonalchanges) that have been stated scientifically to several decimalplaces. If we subtract out the verified components, we are leftwith irregular signals. But the huge migratory storms that crossthe oceans and continents are still out in full force. These aremanifestations of chaos. However, we may be in a periodic statethat lasts longer than the length of our weather records.

So, in attempting to forecast the tides, we are trying to predictthe regular responses (which are already "predictable").But in attempting to forecast the weather, we are met with manychaotic episodes involving the irregular (often "unpredictable")external forces; making accurate advance weather forecasting verydifficult.

Chaos and the Stock Market

Stock markets are another example of non-linear, dynamic systems.Chaos analysis has determined that stock market prices are highlyrandom, but with a trend. The amount of the trend varies frommarket to market and from time frame to time frame. One conceptin chaotic systems is fractals. They are objects that are "self-similar"in the sense that the individual parts are related to the whole.It has been shown that major recessions mimic both monthly anddaily price fluctuations; showing that it is self-similar fromits largest to its smallest scales. The daily, weekly and monthlymarket statistics are all related to the entire market. It is,in a sense, a tree showing more and more detail as it "branchesout". And the predictions of the stock market, like the ever-changingweather, are also dependent upon initial conditions. That is whythese markets are so often difficult to predict.

The complexity of the components of the stock market changes sorapidly, that accurate predictions are almost impossible. Theshort- term data is random and very hard to predict. However,the long-term data is not random and is more easily predicted.But the short-term data accumulates to make the long-term data;so one would think that the short-term data would be predictablelike the long-term. But this is a paradox that shows a systemcan be random in the short-term and deterministic in the longterm. Chaos at work.

Chaos and the Consumer

Chaos theory even plays a part in todayÌs consumer worldmarket. In 1993, The Goldstar Company created a "chaoticwashing machine". It was the worldÌs first consumerproduct to exploit "chaos theory". The washing machinewas supposed to produce cleaner and less tangled clothes. (Byway of identifiable and predictable movements within the nonlinearsystem of the washing machine.) A small pulsator that rises andfalls randomly as the main pulsator rotates, is the key to thechaotic motion. The company expected to make a huge profit andup their share of the world market when they released this product.But, as usual, in the world of consumer sales, another companymade a similar appliance a few years earlier. The Daewoo Companyused "fuzzy logic circuits" to control the amount ofbubbles and turbulence in their washing machine. Fuzzy circuitsmake choices between the numbers zero and one, and between trueand false. This idea was used to control the chaotic conditionsof the washing machine.

Chaos and the Solar System

Astronomers have known for a long time that the solar system doesnot run with great precision. There are certain kinds of instabilitiesthat occur throughout the solar system. Some examples of theseinstabilities are the motions of SaturnÌs moon Hyperion,the gaps in the asteroid belt between Mars and Jupiter, and theorbits of the systemÌs planets themselves.

To astronomers, chaos means an abrupt change in some propertyof an objectÌs orbit. One of SaturnÌs moons, Hyperion,is in a chaotic state. It is not defying NewtonÌs lawsof gravitation and dynamics. Its orbit is precise and regular,but its attitude in orbit is not. It is tumbling over in a verycomplex, irregular pattern.

HyperionÌs position in orbit and its attitude are determinedby the same physical laws and mathematical equations. Its positioncorresponds to a regular solution of those equations; but itsattitude corresponds to an irregular solution. The attitude isthe directions in which itÌs three axes point. Hyperionis not the typical spherical shape of most moons. It is elongatedand irregular, much like a potato. Its shape does not affect itschaotic position.

Every solid body, no matter what its shape or density, has a correspondingellipsoid of inertia. It is a ghost-like anomaly that is rigidlyattached to the body, but has no mass. The lengths of each axisof the inertial ellipsoid are proportional to the inertia of thebody when spun about that axis; so long axes correspond to greaterinertia. The ellipsoid moves along with the body. When the bodytumbles, the ellipsoid tumbles. But suddenly, the ellipsoid absorbsthe material essence of the body, so we now have a solid ghostand a spectral body still attached to it. But the body and itsghost have the same inertial properties, so their motion is identical.

In order to make the best possible prediction of HyperionÌsfuture motion; scientists would have to formulate a complex mathematicalequation for accurate predictability. The Voyager 1 satellitewould make some calculations when it passed over Hyperion. A fewmonths later, Voyager 2 would do the same; and the calculationswould be compared. The predictions were not comparable. The motionsseemed random, yet, were not. Hyperion is in dynamical chaos.

Chaos and Fractals

The name ÎfractalsÌ comes from the Latin ÌfractuaÌ,which means irregular or broken. Benoit Mandelbrot, a French mathematician,started using the phrase in 1975 to describe the pictures he wasseeing that showed the infinite complexities of real rugged systems.Fractals, short for "fractional dimension", embracethe forms of geometry in nature that have been studied for thousandsof years, yet were unable to be described scientifically.

Many of the forms of nature do not fit the mold of the typicalgeometric shapes that we are familiar with. For instance, cloudsare not spheres, bark is not smooth, mountains are not cones andcoastlines are not circles. They do not

have a natural number dimension, as in conventional Euclideangeometry, but have a "fractional dimension". Fractalgeometry is the concept that came about because of this phenomenon.

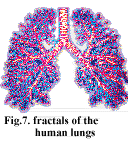Thetheory of fractals applies to many areas of science and technology.Fractals visually describe and analyze the physical forms of coastlines,trees, mountains, clouds, galaxies, rivers, weather patterns andeven the human bodyÌs organs such as the heart, brain,and lungs.

A fractular pattern looks the same whether or not it is viewedfrom a distance or close and magnified. A coastline is an exampleof a self-similar shape, a shape that repeats itself over andover on different scales. How does one actually measure a coastline?The true, actual length of a coastline is infinite. In measuringwith a larger scale map, the process of repeating leads to a greaterestimate of length. Directly measuring the coast would resultin even greater estimates. This fact shows that as the scale decreases,the estimated length

increases without limit. Therefore, if the scale of the measurementswere to be infinitely small, the estimated length would becomeinfinitely large.

A mountain range isanother good example of this concept. From a distance, mountainslook like very large, rugged areas with similar, smaller areaswithin. A closer look will also show a similar pattern, just ona different scale. The mountains look much larger, and the smallerareas appear to be a smaller version of mountains and rocks. Thecloser you get, the more shapes you begin to see within the physicalmakeup of the mountains. The rocks have formations on them, andthe smaller stones have yet smaller formations. These smallerpatterns still resemble the original patterns viewed from a distance,only on a smaller scale.

Benoit Mandelbrot thought that fractals were a way to deal withproblems of scale in the real world. He defined a fractal to be"any curve or surface that is independent of scale, characterizedby their built-in self-similarity in which a motif keeps repeatingitself on an ever-diminishing scale". This property meansthat

any portion of the curve, if blown up in scale, would appear identicalto the whole curve. The same property applies to a "picture",rather than a curve. The

picture, enlarged to scale, would appear identical to the smallerpicture. The transition from one scale to another is representedas iterations of a scaling process.

Fractals are a way to visualize chaotic behavior. Benoit Mandelbrotagain discovered a chaotic pattern in a study of line interference.He found that the bursts of interference had similar, tinier burstsof interference within it. Within each pattern, more similar patternswere detected on each level. He had found the pattern, or order,underlying the chaos.

The Future of Chaos Theory

Another mathematician, Pierre-Simon de Laplace, believed thatif we had an accurate measure of the state of the universe andknew all of the laws that govern the motion of everything, thenwe would be able to predict the future with near perfect accuracy.

But we now know that this is not true. Science was mistaken inits assumption that everything is either a fixed point or a limitcycle. Chaotic systems are not just exceptions to the norm, butare, in fact, more prevalent than anyone could imagine.

The subject of chaos is very exciting to scientists and mathematicians.The movers and shakers of the scientific world want to be thefirst to discover or prove something new in the world of chaos.It is fashionable. It moves very fast. It cuts across numerousdisciplines. These circumstances indicate that we must be carefulof misunderstandings. Good ideas can become discredited if attemptsto apply them are made by people who donÌt understand thepitfalls. This happens often in Îbandwagon scienceÌ.A research team definitely needs a well-informed mathematicianas a team member.

But too much unbridled speculation (trying to forecast stocks,races, etc) could damage the truly useful understanding of chaos.The true description is deterministic chaos, that is, hidden structurein apparently random systems. This theory does not imply thateverything that looks ÎchaoticÌ must have a hiddenexplanation. Only those things that have an underlying deterministiccause are actually chaotic. The base is still mathematics.

Chaos is everywhere and in everything. From the air that we breathe,to the wobble of planets, to the motion of a child swinging ona playground swing, chaos is in abundance.

We now live in an age of great change. Modern scientific researchis at an all-time high. Who would not want to be able to moreaccurately predict the movement of the Earth in relation to naturaldisasters? Hundreds of thousands of lives would be saved if wecould accomplish this feat. More lives could be saved with thestudy of chaotic episodes in medicine involving the human body.Future study is definitely in the works for this relatively newscience. Hopefully, we have only good for mankind to obtain fromthis research.

Book References

Does God Play Dice?, The Mathematics of Chaos by Ian Stewart

The Essence of Chaos by Edward Lorenz

Chaotic Dynamics by G. Baker and J. Gollub

Chaotic Dynamics of Non Linear Systems by Neil Rasband

Turbulent Mirror by John Briggs and David Peat

Chaos, Making a New Science by James Gleick

Mathematical Ideas by Miller, Heeren and Hornsby

Internet References

//tqd.advanced.org/3120/text/gas.htm (Accessed 11/13/99)

//tqd.advanced.org/3120/text/s-market.htm (Accessed 11/13/99)

//tqd.advanced.org/3120/text/washmach.htm (Accessed 11/13/99)

www2.kanazawa-it.ac.jp/t-sutani/pofchaos-e.htm (Accessed 11/22/99)

//members.tripod.com/~SPConnection/nature.html (Accessed 11/30/99)

//members.tripod.com/~planet_e/thirdeye.html (Accessed 11/30/99)

//members.tripod.com/~xinsun/index.html (Accessed 11/30/99)