![]()
![]()
Math Department, Mission College, Santa Clara, California
Go to Math Dept Main Page | Go to
This paper was written as an assignment for Ian Walton's Math G - Mathfor liberal Arts Students - at Mission College. If you use material pleaseacknowledge it.
To explore other such papers go to the Math GProjects Page.
|
|
|
|
|
|
| ~580 B.C. to ~500 B.C. |
| Math G Dr. Ian Walton Compiled By: Nazih Malak Date: 02-May-01 |
Pythagoras is considered tobe the first real mathematician. As an extremely important Greek philosopherand mathematician and founder of the Pythagorean School, but very fewinformation is known about him and his life. The Pythagorean view of the worldconsisted of a belief that numbers were the keys to the various qualities ofmankind and matter. In the Pythagorean view, everything was composed ofnumbers, the explanation for any objects existence could only be found innumbers. This was a completely novel concept, because at that time, numbersexisted for practical purposes only, as a device for solving problems incalendar construction, building and commerce. Pythagoreans were the first whosaw a number as an idea, important in itself. They also made a distinctionbetween logistic (art of computation) and arithmetic (number theory).
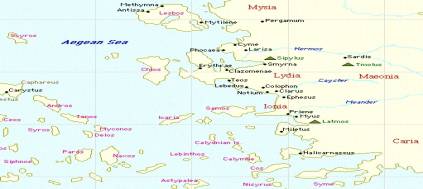
Pythagoras wassupposedly born about 569 B.C. on an island of Samos, Ionia, located in theAegean Sea (see map below), although others will only estimate his birth betweenthe years of 550 or 560 B.C.
Pythagorasbirthplace
At firstglance, there seems to be a great deal of biographical material on Pythagoras,dating from the first centuries of the Christian era; but when history isstudied more closely, the information is fairly vague. Unlike many later Greekmathematicians, there are no documented writings attributed to Pythagoras. Itis believed that this is due to a society which he led, half-religious andhalf-scientific, which followed a code of concealment and therefore caused himto remain somewhat of a mysterious figure in history. It has been stated thatthose facts that we do know about Pythagoras may be unreliable, because many ofthe accounts of this great scholar carry an almost unreliable character. Agreat deal of material is still, to this day, considered legend and or myth.Sometimes Pythagoras is represented as a man of science, and sometimes as apreacher of mystic doctrines. Although some claim this to be a contradiction inideology, most historians feel that the union of mathematical genius andmysticism was actually a common bond, valid and necessary for the times inwhich he lived. The detailed accounts of how Pythagoras invented the musicalscale, performed miracles and pronounced prophecies further enhance theromantic mystique that surrounds his name.
Pythagoras' father's namewas Mnesarchus and his mother's name was Pythais.Mnesarchus was a merchant fromTyre (modern Lebanon), who supposedly brought corn to Samos at a time of famineand was granted citizenship of Samos as a mark of gratitude.As a childPythagoras may have spent his early years in Samos but is known to havetraveled widely with his father. There are accounts of Mnesarchus returning toTyre with Pythagoras. It is then believed that in Tyre, Pythagoras was taughtby Chaldaeans and the scholars of Syria. It is also documented that he was welleducated, learning to play the lyre, learning poetry and reciting Homer.Although all accounts of his physical appearance are likely to ambiguous, therewas one common description that is consistent in all the accounts. Pythagorashad a "striking" birthmark on his thigh.
There areconflicting viewpoints on which of his teachers had the most effect andinfluence on Pythagoras while he was a young man. One of the most important wasPherekydes who was widely believed to be the ultimate teacher of Pythagoras.The other two main figures who were considered to be a major influence onPythagoras and, at some point, introduced him to mathematical ideas were Thalesand his pupil Anaximander. Thales is accredited with influencing Pythagoras'interest in mathematics and astronomy, going as far as to advise him to travelto Egypt to learn more of these subjects. He was however, an old man by thetime they had met and although he did contribute to Pythagoras' ultimatedevelopment, he was probably unable to do more than steer him in a rightdirection. However, Thales' pupil Anazximander gave lectures in Miletus, whichPythagoras attended. Anazximander's lectures on geometry and cosmology and avariety of his other ideas were certain to influence Pythagoras' own views. Onepopular theory states that Pythagoras became a disciple of Anaximander, hisastronomy becoming a natural development of Anaximander's. His geometry is alsosaid to have descended from the teachings in Miletus.
To bettervisualize Pythagoras place on a historical timeline, the following chart servesas a good illustration. It shows the period between 600 BC and 200 BC, whichallows us to see Pythagoras place in the sequence of other philosophers andmathematicians of the period.
In 525 B.C.,Cambyses, the King of Persia, invaded Egypt. Polycrates abandoned his alliancewith Egypt and sent 40 ships to join the Persian fleet against the Egyptians.Cambyses won the Battle of Pelusium in the Nile Delta and captured Heliopolisand Memphis causing the Egyptian resistance to collapse. Pythagoras was takenprisoner and brought to Babylon. While prisoner, Pythagoras became anappropriate student in the sacred rites of the Magoi and learned their mysticalworship of the gods. He also reached what was considered the epitome ofperfection in arithmetic and music and the other mathematical sciences taughtby the Babylonians. In approximately 520 B.C., Pythagoras left Babylon andreturned to Samos.Historians were not able to find any documentation on how hewas able to obtain his freedom. Pythagoras made a journey to Crete shortlyafter his return to Samos to study the systems of laws there. He then returnedand founded a school, which was called the "Semicircle." Drawing onthe notion that all the philosophers before him had ended their days on foreignsoil, Pythagoras decided to make his home in Crotone, a town in Southern Italy.Once at home in Crotone, Pythagoras founded a philosophical and religiousschool. Pythagoras was the head of that society with an inner circle offollowers known as mathematikoi. They lived permanently with Pythagoras and theSociety, had no personal possessions, and were vegetarians. They obeyed strictrules:
1) At its deepest level, reality is mathematical in nature.
2) Philosophy can be used for spiritual purification.
3) The soul can rise to union with the divine.
4) Certain symbols have a mystical significance.
5) All brothers of the order should observe strict loyalty andsecrecy.
Throughout all ofhis teachings, Pythagoras proclaimed himself a philosopher, rather than amathematician. The circumstances of his death are unclear but his legacy liveson. Pythagoras and the early Order initially treated numbers concretely, aspatterns with pebbles, but over time the Pythagoreans developed and refinedtheir concept of number into the same abstract entity, which still existstoday. Though it is difficult to separate fact from fancy in some of thesurviving references to the Pythagoreans, it is generally conceded that theybegan number theory, and were responsible for the introduction and developmentof number mysticism in Western Society.
To thePythagoreans, each number possessed its own special attributes. See for examplethe table below.
| Number | Property of the number |
| |
| 1 | monad(unity) generator of numbers, the number of reason |
| 2 | dyad(diversity, opinion) first true female number |
| 3 | triad(harmony = unity + diversity) first true male number |
| 4 | (justice, retribution) squaring of accounts |
| 5 | (marriage) = first female + first male |
| 6 | (creation) = first female + first male + 1 ? |
| 10 | (Universe) tetractys |
significance in that theirsum accounted for all the possible dimensions:
| | Geometric property | Geometric shape |
| 1 | generator of dimension |
|
| 2 | line of dimension 1 |
|
| 3 | triangle of dimension 2 |
|
| 4 | tetrahedron of dimension 3 |
|
The Pythagoreansare also often thought by various historians to have discovered amicable numbers.Two numbers are amicable if each is the sum of the proper divisors (that is allthe divisors except the number itself) of the other.
For example 220 and 284 areamicable since the sum of the proper divisors of 220 are 1 + 2 + 4 + 5 + 10 +11 + 20 + 22 + 44 + 55 + 110 = 284 and the sum of the proper divisors of 284are 1 + 2 + 4 + 71 + 142 = 220. Superstitious people believed that twotalismans bearing this pair of numbers would seal a perfect friendship betweenthe wearers. The pair also became significant in magic, sorcery, and astrology.
Other numbers thatwere assigned mystical powers by the Pythagoreans were the perfect, deficient,and abundant numbers.
Fortunately, indeveloping their number mysticism, the Pythagoreans also valued proof. To thisend they searched for the essential properties and definitions of many numbers.The following is a brief description of their ideas about numbers:
- The monad is described as limiting quantity, or as the common part or beginning of how many.
- The Pythagorean definition for a number was essentially that number is a collection of units.
- The Pythagoreans made the distinction between odd and even numbers.
Many superstitionsbecame associated with the odd and even numbers. For example the odds weregenerally regarded as masculine and divine, while the evens were consideredfeminine and thus earthly and human. An interesting fact is that due to theinfluence of Pythagoras, the Pythagoreans welcomed women into their Society,and that Pythagoras' wife, Theano, was considered an accomplished mathematicianin her time. Theano and her daughters are believed to have carried onPythagoras work after his death.
- Early Pythagoreans described what we would call prime numbers as "prime and incomposite numbers" and it was generally accepted that a prime number was "measured by no number, but by a unit only", though there was some disagreement about whether 2 was prime. The composite numbers were those which were "measured by any less number". In keeping with the early Pythagorean view of number as a pattern of stones, prime numbers were also called rectilinear because they can be represented as a line of stones only, compared to the composites which can also be arranged into equal size groups of stones. Composites were further distinguished as plane or solid.
- Another legacy bequeathed unto us by Pythagoreans are polygonal or figurate numbers. In fact, when we refer to numbers as figures in modern-day English, we are using the jargon developed by the Pythagoreans. Pythagoras believed that each number is formed by a collection of units it consists of. He used pebbles to illustrate the composition and figure of any given number:
| Figurate Number | Geometric shape |
|
| triangular numbers | |
|
| square numbers | |
|
| pentagonal numbers | |
|
| oblong numbers | |
|
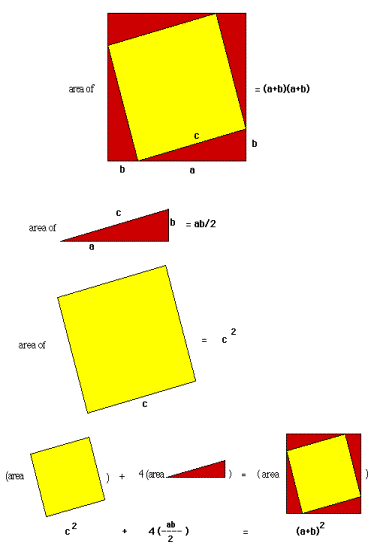
Let us put the Pythagoreantheorem to the test.In a right triangle ABC (C is the right angle), a = 12 cm,b = 7 cm.Find the length of the hypotenuse, c.
2)
3)
Althoughit is difficult to separate Pythagoras personal discoveries from those of theSociety of his disciples, who tended to attribute their own discoveries to him,the fact remains that Pythagoras was responsible for a substantial amount ofrevolutionary ideas and concepts that helped channel the areas of Mathematics,Geometry and Music in the general direction being followed today. To givecredit where it is due, we must acknowledge, that although there areindications that some of the concepts attributed to Pythagoras were known toancient Babylonians prior to his time, the clear formulation of these conceptsand the cohesive force needed to integrate and synthesize theory from thoseconcepts must be attributed to Pythagoras and his followers.Considering thepervasive influence of Mathematics on nearly every aspect of modern life, it isdoubtless that Pythagorean ideas played a major part in shaping the face of ourmodern world!
Bibliography