Math Department, Mission College, Santa Clara, California

Go to Math Dept Main Page | Go to Mission College Main Page

This paper was written as an assignment for Ian Walton's Math G - Math for liberal Arts Students - at Mission College. If you use material from this paper, please acknowledge it.

To explore other such papers go to the Math G Projects Page

Sally McMullen

Math G/Spring ‘09

Dr. Walton

5/11/09

The Golden Touch: An Exploration of the Golden Mean!

“[The Golden Ratio is a universal law] in which is contained the ground-principle of all formative striving for beauty and completeness in the realms of both nature and art, and which permeates, as a paramount spiritual ideal, all structures, forms and proportions, whether cosmic or individual, organic or inorganic, acoustic or optical; which finds its fullest realization, however, in the human form.”

~ A.Zeising 1854

When thinking about what topic I would most like to explore and learn about for my final paper for Math G, I was felt lost. During this semester, we have learned about so many complex mathematical approaches, theories, functions and applications, it has often left my head in a whirlwind of hazy confusion and a desire to spend the time to learn more! Out of any of the classes that I have taken since I decided to come back to school to finish my degree, none have challenged me as much at this one. My appreciation for what we have been exposed to and the fact that I have understood a good majority of it is truly amazing to me! For the first time ever I thought, “Maybe I would even try another type of math class sometime in the near future.” Originally for this paper, I was playing around with the idea that I would like to learn how algorithms in music are traced by computers that are programmed to ‘learn’ music and identify it. I was looking into the software designed by the UK Company Shazam (www.shazam.com) and also the internet radio company Pandora (www.pandora.com). To put it simply, the math is very hard to follow and way over my head! I do however greatly appreciate the Master Minds behind it! I did find that my desire to know how the ‘math-part’ of something could be applicable to a ‘real-life’ practice outweighs my interest in just the knowledge of math applications. There has been one constant that has drawn my attention as it is fundamental in all things in our planet and even beyond!

One such theme, which has been very well covered by my fellow classmates, is that of the ‘Golden Mean’. While we have had numerous speeches where the a lot of the same topics have been discussed, I still am intrigued by what is known as the Fibonacci Sequence, Phi, and the various ‘Golden’ areas, such as the Golden Ratio, and the Golden Section or Golden String. The above mentioned terms are all interconnected and can be found is such a vast array of areas. Since the math for these phenomena have been around for a very long time, it’s safe to say that it has been very well covered! But what fascinated me is that the Golden Mean can be found in such numerous areas that generally are thought of as very separate subjects. In this paper I will explore some very ‘standard’ and commonly know areas that pertain to the subjects discussed above, and I will also expand on areas that I feel are a little less well known which in my research I have found out so much more about! We shall look at nature, and humans as well as environmental finds, and extend it onto architecture, artwork, and then how it blends into advertising and psychology, and then into music.

The essence of the idea of number sequencing and what was later referred to as Fibonacci Series and then the Golden Ratio have long been known of before they were ‘named’ so and applied in their various ways. In a poem that dates roughly back to the 2nd century AD and was translated into Greek in around the 4^th Century, it demonstrates how the basic idea of the Golden Ratio was found in all things, and was regarded mystically and religiously. This is fascinating because during this time period this area was influenced by Greek, Persian-Babylonian and Egyptian cultures, so the combination of all these great intellectual cultures gave way to a highly developed mix of societies. The poem, "All Things are Three" is bewitching and really draws in the concept of just how magical this phenomenon is:

The Monad is enlarged, which generates Two.
For the Dyad sits by him, and glitters with Intellectual Sections.
And to govern all things, and to order all things not ordered.
For in the whole World shineth the Triad, over which the Monad Rules.
This Order is the beginning of all Section.
for the Mind of the Father said, that all things can be cut into three,
Governing all things by mind.
........
The Center from which all (lines) which way soever are equal.
for the paternal Mind sowed Symbols through the World.
...........
Fountain of Fountains, and of all Fountains.
The Matrix containing all things . . .(1)

Even back then, the concept of a divine power, ‘The Monad’, is seen as God and how it can produce two that are ‘intellectual’ and gives order to the creation of all things. The idea that everything can be divided into three parts, and that all lines are equal and that it is a pattern found thought the world in all things. It leads us in believe that it is in fact ‘The Matrix’ of totality itself.

The fact that these cultures all have examples and documented evidence that they all used the Golden Mean which has links to The Fibonacci Sequence and Phi, it is so commonly found that no source will claim to have ‘discovered’ the concept first. The best way I found it put was like this, “It is reasonable to assume that it has perhaps been discovered and rediscovered throughout history, which explains why it goes under several names.” (4) As we move further along with toward the central focuses of this paper I feel it that a we should take a look at what a Fibonacci Sequence is, and how it came to be.

Born Leonardo Pisano Bigollo, was born in Pisa, Italy in ca.1175. IT is said that he was renamed Fibonacci after his father, who was, “Guglielmo Bonaccio. As such, in 1828, centuries after Fibonacci's time, Guillaume Libri invented the name "Fibonacci" from ‘filius Bonacci,’ latin for ‘the son of Bonacci.’ Fibonacci, as he is called by most today, is therefore, just a short version of "filius Bonacci." (5) He apparently spent most of his childhood in North Africa, due to his father’s job as a customs officer. Since his father wanted him to follow the same profession, calculations and mathematical skills where taught to him and was based on a ‘Hindu-Arabic’ system. Given his environment of math and calculations, he came up with a theory of sequencing that was influenced by the question of breeding rabbits:

It makes more sense when you see that the pattern is derived by addition:

1 = 1 + 0
2 = 1 + 1
3 = 2 + 1
5 = 3 + 2
8 = 5 + 3
13 = 8 + 5
21 = 13 + 8
34 = 21 + 13
55 = 34 + 21

There is not finite end for the Fibonacci Sequence, it is a cardinal number that is infinite and represented by : , which is the smallest set of infinite numbers. While the patter looks very simple, and the basic steps of it are: add the last two numbers to get the next. It gets more and more complex and has kept mathematicians up at night for several hundreds of years! This stage as just climbing the ladder to the diving board!

We can demonstrate this sequence by drawing a figure with correlating shapes similar in ratio to the Fibonacci numbers. We can see that the sequence is taken by adding the two numbers together to get the next. The same can be done using squares: 1 and 1 equal 2, 1 and 2 are 3, and 2 and 3 are 5…and so on. These create an outwardly “outwardly spiraling” (5) pattern. It is important to see that the combination of the squares start to for a rectangle as they spin out. They are almost perfectly they same shape.

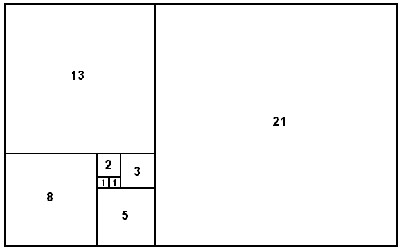
“Notice also that the ratio of length to width is at every step the ratio of two successive terms of the Fibonacci sequence, that is, the ratio of the greater one to the lesser. These ratios may be thought of as forming a new sequence, the sequence of ratios of consecutive Fibonacci numbers: (4)

The algebra gets more complex, but ulimately, what Fibonacci was working towards was the same concept that the Greeks called, The Golden Mean.

Fibonacci Sequence Formula is this:

F(1)=1
F (2)= 1
F (n) = F (n-1) + F (n-2) for n > 2

Golden Ratio Formula: 1+sqrt(5)/2

Gets more complicated: F(n)=Phiⁿ-(-Phi)^-n/sqrt5
Where The Golden Rectangle for Phi has the value 1.618...

(Formulas adapted from: http://www.missioncollege.org/depts/Math/beard/formulas.htm)

They represented this as (f) Phi or Mu (muP, which was considered to be the most aesthetically perfect proportion to be found in all things man-made. And rectangles that contained this proportion where called, Golden Rectangles. It is unclear if Fibonacci ever made the connection to it’s Greek neighbors golden link, but it’s not just humans that have stumbled across it. As we have touched on Fibonaci seqcencing, and how it relates to the Golden Mean we shall expand on this some more. Previously, I had mentioned that Fibonacci discovered this sequencing due to a problem that came to him in rabbits and their projected breeding patterns; I think it is safe that we recognize that it’s not humans that even invented this concept of the Golden Mean.

Moving on to Fibonacci in nature, we see that Aristotle even wisely knew that it was no invention of man, a medieval scholar by the name of Nicole Oresme was quoted saying, “Said Aristotle, prince of philosophers and never-failing friend of truth:
All things are three; The three-fold number is present in all things whatsoever... Nor did we ourselves discover this number, but rather natures teach it to us.” (1)
Perhaps it was with our strong connection on the natural environment that we have a biological tendency to want to mimic that which we find beautiful. The Golden Ratio is found in the very blue print of nature. From the basic counting structure that we discussed we can see that the Golden Rectangle that we discussed earlier can most readily be found in that of the nautilus shell: 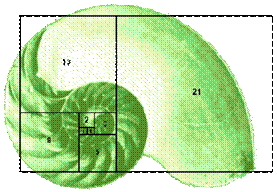(4)

There are many elements in plant life that also follow the Golden Ratio, for example the number of petals that flowers have almost always follow Fibonacci’s sequencing. Ever wonder why it’s so hard to find a four leaf clover? Well, it’s not in Fib’s sequence to start with! Most flowers have petals that go from one: the white calla lily, two are not so common petals are not so common but do occur, mainly they follow the sequence with the highest petal count found in dasies that range from having 55 to 89. It is not for aesthetics that Mother Nature has made plants this way, but for one main reason, survival. It can be best explained in terms of reproduction and seeds. The sunflower is one great example of Fibonacci Spiraling. Just like we talked about above with the nautilus shell, the same sweeping outward patter can be seen in the seed head of a sunflower, and many other plants. The reason is the ultimate Linear Programming for maximum packaging in seeds with the minimum overcrowding issues. There are plenty of other examples of how nature employs the Golden Ratio as an effective tool for survival. And it’s not just in plants and animals!

Here is how the human body also matches the same pattern but in a different way: Imagine that there is a white line from the top to the toes of the body. Now the next line in from marks the length from the head to the finger tips, this is the golden section of the height. The next line in from that marks the distance from the head to the elbows and bellybutton, which is the golden ration of the later. The next line in would be from the head to the pectoral muscles and inner part of the top of your arms. This length also matches length of your shin bones and forearms, and also the width of your shoulders. You can test this yourself by measuring your foot to your forearm; they should be about the same size too. I also remembered an example from in elementary school, that if you take a piece of string and wrap it around your head three times, it will be approximately equal to that of your height.

These proportions of the human frame were considered ‘The Divine Proportion’ and the utmost qualities of true beauty. It should be of no surprise that the laws of the Divine Proportion, and finding the Golden Rectangle in things natural and what we create all have properties that are proportionate to Phi (1.61803398875) which is derived from the equation: 1+sqrt(5)/2. Keep in mind that this is Phi of a rectangle and not a circle! As, our divine universe uses the Golden Touch in all things, for practicality, we humans uses it purely for aesthetic reasons. Or do we? What is it that we find to be attractive in another mate? or a beautiful work of art? Artist have created masks and painted figures for centuries of the ‘ideal’ beauty. As for the face, German Psychologist Gustav Theodor Fechner conducted an experiment in the 1860’s to try and determine if there was, in fact, a direct link between the face with rectangular angles closest to 1.61803398875 where picked out of a group of selected faces with different ranges in the angles and proportions. (7) The results were quite impressive, as out of the ten purposely selected pictures a majority of 76% the total 3 choices were the three rectangles with the ratio of 1.75, 1.62, and 1.50. It is important to note, that these results are not always commonly reproduced, and the consensus of the Golden Ration equaling beauty is debatable. However, what is deemed as Hollywood’s most attractive celebrities all have a similar proportion of golden rectangles in their facial structure. The ideal that ‘beauty is in the eye of the beholder’ best stands to mark attractiveness.

What is deemed as an attractive weight is a highly debatable issue that takes into consideration the wealth of a society and resources available; when food was hard get being what would be ‘fat’ now was a sign of good virtue and health. Now it seems in our excess of fast food and obese gluttony the opposite is deemed attractive, skinny enough to need medical attention! Overall, what women and men find most attractive in the physical form is a healthy balance and proportion in form. As mentioned before, with the human form, there is a correlation between proportions of the breast, waist, and hip size in women and what men find most attractive. Regardless of what is fashionable on film and in magazines, findings have shown that most men are attracted to a body type that is within the closest range of proportions that are congruent with the Golden Ratio. This is because; this ideal shape represents the most ‘fertile’ shape for reproducing and good health; which is a direct correlation to why Mother Nature also uses this proportion as well, I believe it is Darwinism. Men and women both seek this proportion for mating, and it is stimulated by an area in the brain called the ‘fusiform gyrus’ and neurons in this area light up when it is stimulated by what is seen as attractive to the patient. (7) But it is not just limited to human stimulus, as it can relate to things such as automobiles, art & architecture, and plants and animals.

I would also like to include a chart that Norman S. Rose, Ph.D, a child development psychologist and professor at Sonoma State University, related the rate of development in humans to the Fibonacci series:

Human Age	Development Stage	Key Attributes
0	Gestation	Conception
1	Newborn	Birth
1	Infant	Walking, vocalizing
2	Toddler	Talking, expressing, imitating
3	Toddler	Self image and control, toilet training
5	Early child	Formal education begins
8	Mid child	Age of reason, knowing of right and wrong
13	Adolescent	Thinking, puberty, sexual maturation and drive
21	Young adult	Full physical growth, adult in society, education complete, beginning career, financial responsibility,  eligible for voting
34	Mid adult	Refinement of adult skills, parenting role
55	Elder adult	Fulfillment of adult skills, serving, retirement begins with eligibility for Medicare, Social Security and AARP
89	Completion	Insight and wisdom into life

(Borrowed from: http://goldennumber.net/humandev.htm)

Humankinds desire to develop, create and surround itself with the beauty of the Golden Mean, has inspired millions of creative endeavors that can be traced way back in history. The relationship to this subject and my mid-term paper are connected in the fact that my interest in tessellations and tiling stimulate my ascetic sense of beauty. Tessellations and aperiodic tiling stem from the mathematical practice of the Golden Mean and Phi, and it can be seen as a more advanced movement onward from these concepts. Let’s briefly take a look at some of the math behind the architecture and art:

The ratio of the total length of the line (A) to the large section (B) is the same as the ratio of the large segment (B) to the small segment (C)).

In other words, A is to B as B is to C.

This occurs only where A is 1.618 ... times B and B is 1.618 ... times C.

A Greek example of this formula can been seen in the classical structure of the Parthenon:

Figure 1: Adaped from: http://emptyeasel.com/2009/01/20/a-guide-to-the-golden-ratio-aka-golden-section-or-golden-mean-for-artists/

It is speculated that the Egyptians used it in the construction of the pyramids, other cultures followed similar conformations of architecture. Renaissance art and even Modern art use the Golden Ration to proportion their landscape, design faces, or set a scene. As we have been exposed these aspects of the Golden Mean and there relation to the nature of the environment & human form, and art & architecture, and how it effects us neurologically, it is clear that the visual aid in the Golden Ratio is predominate in a plethora of things. This leave us with the remaining subject of gift of audio senses that we posses.

This brings me to the part of the paper that I have been most eager to talk about: Our auditory skills and music and their correlations to the Golden Mean. When looking at Western Music, it is important to know that the standard ‘tempered frequency’ starts at A440 and that with this arbitrary standard it is how the frequency chart relates to the Fibonacci sequencing. This standard pitch was proposed in 1917 and internationally accepted by 1939 (9). I relate it to how the standard of Received Pronunciation was determined around 1914 in England that set how the phonetic alphabet should sound. These standards were set to help people to be able to produce a sound without a direct auditory example of how to do so. Below is a graph that shows the relationship between the Fibonacci sequence and how it correlates to the music scale:

Fibonacci Ratio	Calculated Frequency	Tempered Frequency	Note in Scale	Musical Relationship	When A=432 *	Octave below	Octave above
1/1	440	440.00	A	Root	432	216	864
2/1	880	880.00	A	Octave	864	432	1728
2/3	293.33	293.66	D	Fourth	288	144	576
2/5	176	174.62	F	Aug Fifth	172.8	86.4	345.6
3/2	660	659.26	E	Fifth	648	324	1296
3/5	264	261.63	C	Minor Third	259.2	129.6	518.4
3/8	165	164.82	E	Fifth	162 (Φ)	81	324
5/2	1,100.00	1,108.72	C#	Third	1080	540	2160
5/3	733.33	740.00	F#	Sixth	720	360	1440
5/8	275	277.18	C#	Third	270	135	540
8/3	1,173.33	1,174.64	D	Fourth	1152	576	2304
8/5	704	698.46	F	Aug. Fifth	691.2	345.6	1382.4

Figure 2:Borrowed from: http://goldennumber.net/classic/music.htm

The piano is tuned to fit this scale, however there is still debate as to which is the more natural sound to start out the scale with, being either A432 or C256. As I am not musically educated, I have no idea where to begin with that controversy. Moving, on we look at how music is based on the Fibonacci series with instruments such as the piano:

“There are 13 notes in the span of any note through its octave.
A scale is comprised of 8 notes, of which the
5th and 3rd notes create the basic foundation of all chords, and are based on whole tone which is
2 steps from the root tone, that is the
1st note of the scale. “(9)

This looks very much like what is known as the Golden String:

The Golden String is a fractal string of 0s and 1s that grows in a Fibonacci-like way as follows:

1
10
101
10110
10110101
1011010110110
101101011011010110101

It is important to note that most of the music that has relations to Phi and the Golden Ration tend to be that of a Classical nature. But it is in measuring these things and the set foundation that these theories provide for us are the platform in which companies like Shazam and Pandora use to mark trades in music that we find appealing. For instance, Pandora created a Genome analysis that examines and looks for matches of over 400 parameter traits that are measured the algorithm of one song. These are all done by the human ear, as these traits can be hard for computers to learn to analyze. Just to get a grasp on the types of characteristic traits looked for in each algorithm, I have included a ‘short’ list, as there are about 400 attributes looked for. The more advanced we get in teaching computers to analyze these characteristic themselves, human ears at Pandora will be outsourced!

• arrangement - the selection and adaptation of a composition or parts of a composition to instruments for which it was not originally designed
• beat - the regular pulse of music
• form - the structure of a composition, the frame upon which it is constructed; based upon repetition, contrast, and variation
• harmony - the concordant (or consonant) combination of notes sounded simultaneously to produce chords
• lyrics - the words of a song
• melody - a succession of tones comprised of mode, rhythm, and pitches so arranged as to achieve musical shape
• orchestration - the art of arranging a composition for performance by an instrumental ensemble
• rhythm - the subdivision of a space of time into a defined, repeated pattern
• syncopation - deliberate upsetting of the meter or pulse of a composition by means of a temporary shifting of the accent to a weak beat or an off-beat
• tempo - the speed of the rhythm of a composition
• vamping - to extemporize the accompaniment to a solo voice or instrument
• voice - the production of sound from the vocal chords, often used in music; falls into six basic categories defined by pitch, ranging, from bottom to top, Bass, Baritone, Tenor, Contralto, Mezzo Soprano, and Soprano (10)

The most important thing that I think we should keep in mind is that just as what is ‘attractive’ visually is mainly subjective and to personal discretion, so it what is auditory although similar patterns are found in all music. As an interesting side note as to the power of psychology and mapping what is appreciated by age, I came across a website that provides education in persuasive psychological tactics. A group of local convenience stores wanted to stop teenage loitering around their stores and engaging in fights and drug dealings. Yet, they still did not want to lose the business of the teenagers either. They hired an ‘influence expert’ and were recommended to play a certain genre of music outside the store but not inside the store. The result was successful and the teenagers still remained patrons of the store but no longer ‘hung out’ there. Interestingly the music played was, Frank Sinatra! (9) I was very interested to find out why this was and if it had anything to do with a dislike of certain algorithms in music or something else! Unfortunately, I found no such information as it seems I would need to sign up for the classes offered through this website.

It is not mistake that all of the topics that we covered affect us neurologically, which effects our emotions and even our attention span and intellectual development. The root of all of these aspects; be it of natural and/or human-made occurrence, without a doubt, have strong connections to the fundamental math of the Golden Mean and Fibonacci Sequencing. There is not time to investigate more into these subjects, as I find them fascinated and all so intricately intertwined. As the math that I have mentioned here is very basic, I hope that the examples that I have touched on here, drawn attention as to why it is really such a absorbing topic to consider. For many brilliant minds, and for myself, it makes me question creation and where all these things come from. Is it merely by chance that all things are so connected? Or was it a ‘Divine’ plan? Whatever it is, it is beautiful and should humble us all in terms of our connection with all elements of this planet and beyond.

Book References:

1. The Chaldean Oracles as Set Down By Julianus,{Latin: Francesco Patrizzi; English: Thomas Stanley} Heptangle Books, Gillette, New Jersey, 1939:3

2. Graland, Trudi Hammel "Fascinating Fibonacci's" CA:Seymour Publications, 1987

3.. Vajada, S. "Fibonacci and Lucas Numbers, and the Golden Section." West Sussex, England:Ellis Horwood Limited, 1989

WEBSITES:

4. http://goldennumber.net/classic/history.htm The Evolution of Truth, 1999-2004

http://library.thinkquest.org/27890/biographies1.html

5. http://www.mathacademy.com/pr/prime/articles/fibonac/index.asp

6. http://library.thinkquest.org/05aug/01274/phibeauty1.htm

7. http://www.sciencedaily.com/releases/2008/04/080404122139.htm

8. http://www.mondovista.com/faces.html

9. http://brainmind.com/facearea2.html

10. http://goldennumber.net/classic/music.htm

11. http://computer.howstuffworks.com/pandora3.htm

12. http://www.workingpsychology.com/whatcan.html