Go to Math Dept Main Page | Go to Mission College Main Page

This paper was written as an assignment for Ian Walton's Math G -Math for liberal Arts Students - at Mission College. If you use material from this paper please acknowledge it.

To explore other such papers go to the Math G Projects Page.

  The most important part of the car is unarguably the engine.This is the muscle of the car. The most obvious way to make your enginebetter is to follow the old rule of "bigger is better". For the time beingI will pretend I have a 1963 Corvette stingray that I put a small block350 cubic inch (ci) engine into. I went with the Chevy 350ci engine becauseof its popularity and ease to find specifications on. The engine came stockwith a 4" bore diameter and a 3.48" stroke. The most common way of makingan engine bigger is to bore out the cylinders. Let's take the specificationsof the stock engine and see what happens when we bore it out .060". Tofind the cubic inch displacement of an engine you will use this formula:

In plain english this states that Displacement = Pi÷4 x bore² x stroke x number of cylinders. The answer comes to 349.84777which we round up to 350. Hurray the formula works! Now to put it to workfor us.

  When racing your car you will always have limits to stay withinset by Nascar. The next limit above 350 is 366 set by Nascar's standards.So with this in mind let's see what happens when we bore out our 350ci.The maximum you could go and still be able to find pistons and rings withouthaving them built special is .060" over. With this in mind we re-do ourformula with the new bore size:

And we get our new size of 360.59 or rounded up to 361ci. We are wellunder our limits, so the next step is to add some stroke.

  Putting in shorter or longer piston rods changes stroke. We startedwith a stoke of 3.48. As you can see the measurements here are extremelyaccurate. You could increase or decrease by .01" at a time, a lot of workif you don't have a formula. But then if there were no formula, I probablywouldn't have mentioned it. So here we go:

Looking at this formula you will see some old familiars. We have simplychanged our last one to include the .060" overbore and are dividing itfrom 366, our maximum engine size. Working the math out gives us an answerof 3.53247 or 3.53 rounded down. We now have done all we can to the engineblock and have gotten the maximum allowed out of it.

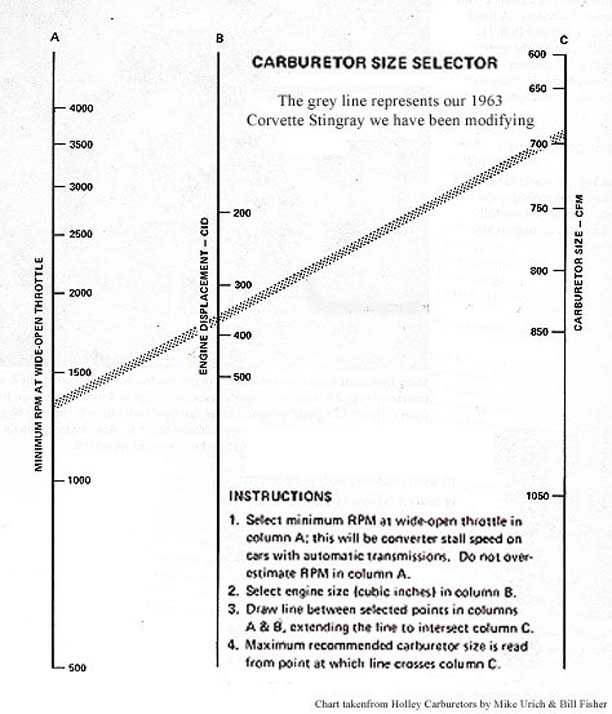
Now that we have our block right where we want it we can start addingon the rest of the engine to match. The best place to start here is withthe carburetor. Once you pick out a carburetor the rest of the "bolt-onperformance" parts, such as exhaust hedders and intake manifolds, willbe matched to it. The people at Holly Carburetors have done us a greatfavor in figuring out the math for us and creating an easy to use chartfor choosing the right carburetor. I have used our previous car and modifiedengine with this graph and you can see it comes out to be almost 700 cfm.The Stingray being a smaller, lighter car than most Chevy's we can go aheadand round up without loosing horsepower.

Now if you are not one to put your new built engine and hard earnedmoney into a carburetor just on the advice of a graph, there is a way tofigure out the math yourself:

Putting this to work with our new hot rod we know that the CID (cubicinch displacement) is 366÷2 = 183. Our RPM is 6600 as I'll explainlater. Divide that by 1728 giving us 3.8194. Multiply those two figurestogether, 183 x 3.8194 x volumetric efficiency, which we will assume is100%, or 1 converted to decimals, since we just built it, we get an answerof 698.95 which again we will round up to 700 cfm, the same as the chart.

  Once we have our engine built to specs it's time to get the carrolling. Choosing the right Transmission will depend on the type of racingyou will be doing. I've chosen the Borg-Warner for two reasons: No modificationwill need to be done to attach it to the motor, and it's a great transmissionfor the drag strip. The first bit of math that you will need to understandbefore any other, are gear ratios. Simply put, this is the difference betweenthe input gear, connected to the engine, and the output gear, connectedto the final drive that turns the wheels. With a transmission you havegears with teeth so no actual measurements have to be made. All you dois count the teeth on both gears and divide the number on the driven gearby the number on the driver gear. The gear ratios for our Borg Warner transmissionis as follows:
 

1st gear = 2.20:1 2nd gear = 1.66:1 3rd gear = 1.31:1 4th gear = 1:1 (or direct drive) With that information and the dyno chart and just two more equationsyou can build a chart of your own to find the optimal shift point. I'llgo through that now step by step. First step for building a chart is tofind out what RPM you will be at after you shift. Dividing the gear ratiosand then multiplying that with the RPMs before the shift does this. Theequation comes out to this: RPM After Shift = (ratio shift into ÷ ratio shift from) x RPMbefore shift

RPM 3000 3200 3400 3600 3800 4000 4200 4400 4600 4800 5000 5200 5400 5600 5800 6000 6200 6400 6600 6800 7000 FT LBS 340 340 345 345 350 350 340 335 330 325 315 310 305 305 305 300 280 255 240 190 160 BHP 194 207 223 236 253 267 272 281 289 297 300 307 314 325 337 343 331 311 302 246 213

Using our gear ratios for the Borg Warner transmission we can figureout what the RPMs will become after shifting from 1st to 2nd at 6000 RPMs.

The 2nd step to building your chart will be taking the results of thebrake torque foot pounds of the engine from the dyno chart and convertingit to shaft torque foot pounds, at the wheels. Too much of a loss of torquewill cause deceleration. Too much gain will cause you to loose tractionat the wheels. Both are deadly when it comes to racing. To convert brakeft lbs. to shaft ft lbs., it is as simple as multiplying the brake ft lbs.by the gear ratio of the driven gear:

  Now we have everything we need to build our chart. Set up RPMsranging from 6000 to 7000 in 200 intervals. Then plug in the brake ft lbs.from the dyno sheet. The dyno sheet, by the way, is the only part of thisthat you won't be able to do mathematically. There are simply too manyvariables to the engine to be accurate enough. The only way to get thesefigures is to head down to your local machine shop and have them computeranalyze your engine. So take 6000 RPMs, plug in the brake torque from thedyno sheet, convert it to shaft torque with your new equation. Next, plugin the RPMs after the shift, again using the equation mentioned earlier,find the appropriate brake torque, convert it into shaft torque, and subtractthe difference. Do this with each RPM and each shift point and you comeup with a chart like this:
 

RPM	Brake lb-ft	Shaft lb-ft	RPM	Brake lb-ft	Shaft lb-ft	Loss/Gain
Shift from 2.20 1st to 1.66 2nd
6000 6200 6400 6600 6800 7000	300 280 255 240 190 160	660 616 561 528 418 352	4527 4678 4829 4980 5131 5282	330 330 325 315 310 310	548 548 540 523 515 515	-112 -68 -21 -5 97 165
Shift from 1.66 2nd to 1.31 3rd
6000 6200 6400 6600 6800 7000	300 280 255 240 190 160	498 465 423 398 315 266	4735 4893 5051 5200 5366 5524	325 325 315 310 305 305	426 426 413 406 400 400	-72 -21 -10 8 85 134
Shift from 1.31 3rd to 1.00 4th
6000 6200 6400 6600 6800 7000	300 280 255 240 190 160	393 367 334 314 249 210	4580 4753 4885 5038 5191 5344	330 325 325 315 310 305	330 325 325 315 310 305	-63 -42 -9 1 61 95
Chart figures taken from Auto Math Handbookby John Laylor

Looking at the chart we can plainly see that 6600 RPM is the optimalshift point in all gears. It's a good thing too. Remember we just boughta carburetor using that figure.

  So now we have our hotrod with a strong motor and a matched carburetor,and we know when to shift to get the most out of the wheel torque, butwe're still not winning the races. The reason is we haven't looked at weightdistribution yet. Weight distribution is the final factor that will winor loose a race. For drag racing, the two main factors we will want toknow is center of gravity from front to rear and it's height. Ideally wewant 100% of the cars weight on the rear wheels. This is where all thetorque and acceleration is. Start with front to rear first, as that answerwill be a part of height's formula.

  To find center of gravity from front to rear you need three things:A tape measure, a big scale and this formula:

On our 1963 Corvette, with a wheelbase of 98", and a weight of 2859lbs,we take a reading from a scale with only the rear wheels on, and solvefor F this way:

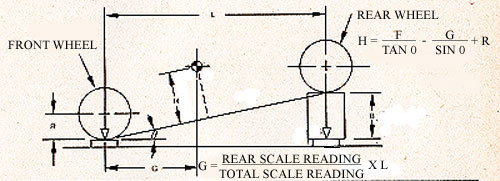
  The center of gravity height gets a bit more complicated in boththe setup and the math. I'll go through step by step using the chart belowas reference. First thing you need to do is set the rear of the car upon blocks, with the scale under them. For our model I have used 2ft blocks.Now take the readings again. For sake of experiment I will say the readingat the rear scale went from 1300 to 1192. Looking at the equation,

we almost have enough information to solve now. The one factor we don'thave yet is L. However we know that our blocks are 24" and our wheelbaseis 98". We can find the 3rd side of the triangle, or L, by using the Theoremof Pythagoras, which states that, in a right triangle, the square of theside opposite the right angle equals the sum of the squares of the othertwo sides. So the 98" wheelbase is the side opposite the right angle. 98squared is 9604. The other known side is 24" blocks. 24 squared is 576.The square of the third side will be 9604 minus 576 or 9028. So the measurementof the third side will be the square root of 9028, or 95.02. By using theformula to solve for G we know that G = 39.6.

  Now we're ready to solve for H using the formula

Using a little trigonometry and our friend Chief Soh Cah Toa, we cansolve tan = 24/95 or 0.25, and sin = 24/98 or 0.24. R is a simple measurement,in our case coming out to 10.5. By substituting our numbers we get an answerof H = 23.74.

  Now we are ready to take those figures with us to the tire shopand suspension garage to have them work their magic. They will be ableto match everything on your car to move the center of gravity back andeliminate tire hop and suspension squatting, and hopefully you will startwinning some races.

  So go out there and have some fun with your car. Just keep inmind this last formula:

This paper was written as an assignment for Ian Walton's Math G -Math for liberal Arts Students - at Mission College. If you use material from this paper please acknowledge it.

HTTP://WWW.NETVETTES.COM/1963.HTML10/20/00

HTTP://WWW.PRESTAGE.COM/CARMATH/DEFAULT.ASP10/05/00

HTTP://WWW.MORTEC.COM/EXAMPLE.HTM10/05/00

Auto Math Handbook Basic Calculations, Formulas, Equations and Theoryfor Automotive Enthusiasts by John Lawlor 1991 HP Books

Practical Problems in Mathematics for Automotive Technicians Third Edditionby George Moore 1985 Delmar Publishers

How to Make Your Car Handle by Fred Puhn 1976 HP Books

Holley Carburetors by Mike Urich & Bill Fisher 1972 HP Books