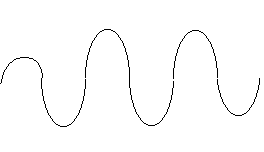Go to Math Dept Main Page | Go to Mission College Main Page

This paper was written as an assignment for Ian Walton's Math G -Math for liberal Arts Students - at Mission College. If you use material from this paper please acknowledge it.

To explore other such papers go to the Math G Projects Page.

Jacqueline Tacorda

Dr. Ian Walton

Math G

23 November 2001

Final Paper

The Mystery of Ocean Waves

"What goes up must come down", (Anonymous). Have you ever watched the waves when you’re lounging at the beach? Of course you have! Almost everyone has had a one-time experience observing the ocean. Whether it be just sitting on the sand looking at the open sea, or watching from a cliff or from a distance, as the waves hits and breaks against the rocks or the cliffs... My point is we all have our own experiences of watching the ocean’s waves. When I think of waves in the ocean, I remember the saying: "What goes up must come down," by an anonymous person. The ocean is a source of escape for most people and everyone has their own perspective on how one perceives the waves. I myself love the ocean, I think waves are fascinating in many ways, but in this paper, I will attempt to discuss how mathematics is involved in studying waves.

In the most basic of all wave properties, a person might ask, "What exactly is a wave?" With my high school science experience, I remember my definition of wave as a traveling disturbance caused by something; it could be a coin tossed in a puddle of water, or the wind rubbing against the surface of the water. Keep in mind that a wave can occur

anywhere other than in water, don’t get thrown off when I say "water". I am only using "water" as my example because my main topic is waves occurring in water, so most of my explanation will relate to waves in water. My definition is rather vague; so let me use P. Erik Gundersen’s definition of a wave. In his book, The Handy Physics Answer Book,

Gundersen writes, "a wave is a traveling disturbance that moves energy from one location to another without transferring matter", (173).

Now, if you’re still unsure what defines a wave, take a piece of rope, and hold it on one end perpendicular to the floor’s surface while the rest of the rope is set dangling free. After, steady the rope, so that it is stationary. Then, begin shaking one end of the rope (the end you’re holding). Did you see what happened? If you tried it, or imagined it, either way, you should have seen a continuous wave that traveled from the top to the bottom of the rope.

Top end of the rope 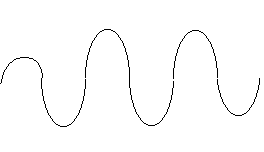Bottom end of the rope

In the figure above, I tried to illustrate how the rope would behave with the instructions I had given previous to the figure. The only difference is, you see the figure above in side view. Let us just assume that the left end of the rope is the top end, and the right end of the rope, the bottom end. Again, in the illustration, we see that when the left end (the tope end) of the rope is shaken, there will be a continuous wave that travels through all the way to the other end of the rope.

Art Hobson in his book, Physics: Concepts and Connections, has the illustration of a wave that I think might be more helpful than the rope example. Hobson describes a sports wave. In his book, he writes, "a sports wave begins when all the people in one

TACORDA 3

portion of the stadium, often at one end, stand up briefly with their hands in the air. As they sit down, the people sitting in the adjoining part of the stadium stand up briefly with their hands in the air, and so forth all around the arena," (192). Now, if you were there watching the crowd, you would see a sports wave manipulated by the people in the crowd. The same idea applies to the waves in the ocean. To sum up Hobson’s example, he writes, "each individual part (each person) of the ‘medium’ (the crowd) simply stands up with hands in the air, and sits back down. The people who are momentarily standing constitute a disturbance of the otherwise-seated crowd and it is this disturbance, rather than any individual person, that travels through the crowd", (192).

Given that we now know how to define waves in this discussion, let me proceed to what type of wave an ocean wave is. In the properties of waves, there are three different types of waves described. They are Transverse, Longitudinal, and Transverse & Longitudinal waves. There are further explanations and terms used within those three types of waves, but I will only discuss transverse, and longitudinal waves because it is those two types of waves that apply to the topic. In an ocean wave, it is a combination of transverse and longitudinal waves that make up the ocean. Gundersen says, "the water molecules in a water wave vibrate up and down in tiny circular paths. The circular path of the water wave creates an undulating appearance in the wave," (Handy Physics 176).

The figure below is from James Trefil’s book, A Scientist at the Seashore. I chose this illustration because I think it helps describe what Gundersen said about how water wave vibrates up and down in tiny circular patterns. Trefil says, "the farther away from the bottom we get, the less squashed the ellipses become," (Scientist 82). Furthermore,

TACORDA 4

Gundersen offers more explanation in his book, he writes: "At the crest of the wave, the water molecules tend to spread out a bit, resulting in an area of rarefaction, while in the trough of the wave, the water molecules are compressed," (Handy Physics 176). In brief, I’ll summarize what Gundersen says... The ocean wave is a combination of both transverse and longitudinal because in the crest, which is the highest tip of the wave, rarefaction (an area after the compression, materials spread out) occurs, and in the trough, which is the lowest part of the wave, compression (an area where it is condensed, materials are thick). The illustration below should give you a better understanding of the previous discussion.

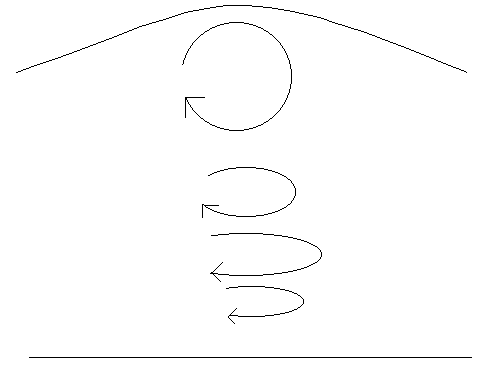
Ocean floor

Source: James Trefil, A Scientist At The Seashore, 82.

TACORDA 5

With all that information given, I think I will be able to discuss how the speed of

a wave is determined. Measuring the speed of wave is where I can apply the mathematics into my topic of ocean waves. Since I am not an expert on ocean waves, and mathematics, I am trying very hard to stay with mathematical applications into the study of waves. I’m sure most of my discussions so far are mostly connected to physics; however, I will try to discuss more "mathematics" in this discussion. I have to admit though, that it won’t be anything "spectacular" and fancy with trigonometry, and algebra (the two types of mathematics that popped up most frequently during the digging process of my research); rather, it will be simple, since with the time allotted I have left, I could not truly understand the more complicated computations I came across during my initial research. Hence, I am comfortable staying within less complicated areas and this is where I think I’ll remain.

Having said that let me move forward to discussing how to determine the speed of an ocean’s wave. The equation for determining the speed of a wave is velocity equals the frequency multiplied by the wavelength (Handy Physics 175). Let’s just define some of these terms. "The wavelength of a continuous, repeated wave is the distance from any point along the wave to the next similar point", (Physics: Concepts and Connections 192). So, the speed the crest takes to move from one crest to another is the wave speed. The same concept applies for the motion the trough makes. "The wave’s frequency is the number of vibrations that any particular part of the medium completes in each second," (Physics 192). So, the frequency can also be referred to as the number of waves the source (the "thing" that sends out the vibrations) sends per each second. We measure the

TACORDA 6

frequency of a vibration per second by using a unit called a hertz, denoted as Hz in most

computations, (Physics 192).

Hobson further explains in his book that "quantitatively, a wavelength l, frequency ƒ, and wave speed s = ƒl," (Physics 192). Hobson also gave the following example below.

Ex.: If three waves are sent out by the wave source every second (ƒ = 3 vibrations per second) and each wave has a length of 2 meters (l = 2 m), then it seems reasonable that the wave speed should be 3 x 2 = 6 m/s (meters per second).

Hobson concludes that by "extending this argument, you can see that the general relation is s = ƒl," (Physics: Concepts and Connections 192).

Gundersen concurs with Hobson; he writes that the relationship between frequency, wavelength, and velocity is velocity = frequency x wavelength. Hobson says, "as long as a wave remains in one medium, the speed of a wave will remain constant. Since the velocity of a wave does not change, under those conditions, the only variables that could change would be the frequency and the wavelength," (Handy Physics 175). Given that the relationship is velocity equals the frequency multiplied by the wavelength; thus, we must assume that when the frequency of a wave is increased, the wavelength has to decrease for the velocity to stay constant. Hobson concludes that "the frequency and wavelength are inversely proportional to each other," (175).

In studying the ocean’s wave, we use the idea of inverses. In our class, we briefly discussed inverses in several different chapters of the book; for example, we discussed inverses in relation to graphs, and in exponential and logarithmic functions. I think the

TACORDA 7

example Hobson gives if not similar, then somehow related to the ideas we discussed in

Chapter seven of our text Mathematical Ideas, that talks about inverse variations. Hobson’s example of how inverse works in relation to frequency, wavelength, and velocity is:

"sound travels at a speed of 331 m/s (meters per second) in air that is at the freezing mark. If the frequency of different sound waves were changed, the wavelengths would change as follows" (175):

Velocity of Sound (0° C) Frequency (Hz) Wavelength (m)

331 128 2.59

331 256 1.29

331 512 0.65

331 768 0.43

Source: P. Erik Gundersen. The Handy Physics Answer Book, 175.

To summarize the table above, Hobson was just trying to illustrate the idea that frequency and wavelength are inversely proportional to each other. In the table above, sound travels at 331 meters per second not considering the sound’s frequency; thus, sound will continues to travel at 331 meters per second until the medium is interrupted by a change. This is illustrated in the first column of the table (Velocity of Sound 0°). On the second column of the table we are given different frequencies, which is measured in unit by hertz. Notice that from the first data entered, the frequency is 128 Hz, then

gradually increasing as more data is fed. By the fourth data entered, the frequency is at 768 Hz, yet still at the same velocity from the first data entered (128 Hz). Again, this is

possible because we are allowing the velocity of sound to remain constant. On the third column, we are given the wavelength, which is measured in units by meters. Take note that the first data entered in this column is 2.59 m with the velocity sound of 331 m/s, and the frequency of 128 Hz, and as more data is given, notice that the wavelength is gradually decreasing. By the last data entered in the wavelength column, we are given 0.43 m at the same velocity of sound (331 m/s) with the frequency of 768 Hz.

To be brief, the idea of inverse is used in the table to describe how frequency and wavelength are inversely proportional to each other. We see this by noticing the changes in data in the second (frequency) and third (wavelength) columns of the table. The inverse idea is visible in the data because as the frequency begins at 128 Hz and gradually increased to 768 Hz and at the same time, the wavelength begins at 2.59 m, however, it does not increase, instead it gradually decreases to 0.43 m. Therefore, it can be said that the frequency and wavelength are inversely proportional to each other because as the frequency increases, the wavelength decreases.

One of the few main ideas from what this class seemed to emphasize is finding applications in things we encounter everyday into mathematics. Well, now that I have discussed how mathematics can be applied into studying waves. There’s also another idea that I came across from one of the books I sourced in this paper, which I thought could be applied to mathematics. In Gundersen’s The Handy Physics Answer Book there was a brief discussion on how downhill skiing is similar to surfing. In my personal experience,

though I have a certain fondness for the ocean, I have never tried surfing before, but I have experienced downhill skiing in the mountains of Sierra Nevada.

Mathematics can be applied to downhill skiing in many different ways. For example, a skier might want to determine how steep a slope is by using vertical and horizontal lines, in relation to positive and negative slopes. So, basically, lines and their slopes are involved. Similarly, mathematics could be applied to surfing. In skiing, the hill is covered with snow, and in surfing the hill is the rising water of an ocean wave breaking (Gundersen). I think both sports could use mathematics in the sense that an athlete can be in an advantage if he/she knew about the differences in slopes in they’re given obstacles.

Another mathematical application I could think of that’s somewhat related to my topic is the study of a tidal wave or tsunami. Tidal waves or tsunamis are caused by volcanic eruptions or underwater earthquakes and not by windy environment like most people believe. Gundersen offers his explanation in his book, "the seismic disturbances create huge upward forces on the water, the opposite of dropping rocks into the water," (Handy Physics 179). Probability can be utilized in the study of tidal waves or tsunamis. As well as the chaotic system we discussed in class.

I remember from the chaos video we watched in class, there was a section where chaos was applied to weather. If I remember correctly, one of the video’s main points was discussing whether or not chaos could be predicted. Well in weather, forecasters have it difficult because they are attempting "to instill order in chaos by predicting the outcome of a weather system," (Handy Physics 352).

Also, since tidal waves or tsunamis are caused by underwater earthquakes or

volcanic eruptions, this means that geologist must apply mathematics in their observations because studying earthquakes uses the Richter scale to rate the intensity of

the earthquake. In our current textbook, Mathematical Ideas, it says that "the Richter scale rating of an earthquake of intensity x is given by:

R = log₁₀ x/x₀

where x₀ is the intensity of an earthquake of a certain (small) size," (483). The text also gives the logarithmic equation given in exponential form:

10^R = x/x₀ or x = 10^R x₀

Now, a person might what to know what the above equations have to do with applications to waves. Well, since tidal waves or tsunamis are not a frequent event, it is still important to study them to gain more knowledge to how we might help prevent the damages it creates, and by studying tidal waves or tsunamis, one must apply mathematics into it.

In conclusion I had discussed how mathematics could be applied in the study of ocean waves. With the use of algebraic equations, one can determine the speed of a wave. Along with the having some information about how inverses behave, one can apply it when analyzing data in relation to frequency, wavelength, and velocity. By studying slopes and linear inequalities one can apply it to surfing the breaking waves or skiing down a snowy mountain. Last but not least, one can apply mathematics in how ocean waves behave with the use of logarithmic equations and chaos.

In the end, "what goes up must come down". Next time you’re lazily laying on your beach towel staring at the ocean, think how amazing it must be to behave like a

wave in the ocean. Myself included (but I’m not very objective because I love the ocean), in any case, I’m quite surprised how much mathematics can be applied to the ocean’s waves. Personally, I knew math was involved somehow because studying waves involves physics and I definitely remember physics having A LOT of math. To get to my point, I was a little surprised how much math was really involved in something I think is truly fascinating (the ocean’s wave). I am not a math person. I’m disappointed to say I do dislike math (ducking from all the math extremist out there), but I’m glad I did my final paper on how mathematics is involved in the ocean’s wave because now, I can walk away from this having a newfound appreciation for math and willingly say, "I don’t dislike math as much as I did two weeks ago."

Works Cited

Gundersen, Erik P. The Handy Physics Answer Book. Detroit: Visible Ink Press, 1999.

Hobson, Art. Physics: Concept and Connections. 2nd ed. New Jersey: Prentice Hall, 1999.

Trefil, James. A Scientist at the Seashore. New York: Charles Scribner’s Sons, 1984.

Heeren, Vern E. , John Hornsby, Charles D. Miller. Mathematical Ideas. 9th ed. Boston: Addison Wesley Educational Publishers, 2001.

This paper was written as an assignment for Ian Walton's Math G -Math for liberal Arts Students - at Mission College. If you use material from this paper please acknowledge it.