In fact, some examples of fractals in nature can be emulated on the computer using a mathematical expression:

The name Fractal was coined by mathematician Benoit Mandelbrot in the 1970's. (You read that correctly -- this area of math is really almost that young!) It comes from the Latin fractus. The verb frangere means to break, to create irregular fragments. Mandelbrot was interested in both meanings: fragment and Irregular, to describe the Math he was studying.

This area of Math falls into the field called Chaos or Dynamical Systems. Fractals are simple, nonlinear systems with complex dynamical properties. There are two distinct types of fractals: Julia Sets and Mandelbrot Sets. There are two characteristics to both Julia Sets and Mandelbrot Sets that are important and should be noted: One is that they have self-similarity. That is, the shape repeats over and over to what looks like infinity. The other is that on the boundary the process is very chaotic. It contains chaotic sequences of points that never approach any kind of regularity.

Both fractals and chaos are branches of math that are currently getting a lot of attention for they are both modern discoveries. They are an area of geometry that parts from the standard Euclidian straight-line geometry. This new geometry has a morphology of it's own. It seems to offer never-ending variations and constantly evolvoing shapes that "morph" from one thing to a completely new and thing. It seems to be chaotic, turbulent and random. In reality, underneath all those beautiful, colorful, undulating shapes there is a simple and basic equation. The basic fractal shape is called a Mandelbrot and it's expression is deceptively simple: x² + c. (More on this later.)

The really interesting part of a fractal to look at is actually the boundary area between a black center region and colorful outer areas. It is this boundary which seems irregular and fragmented that Benoit Mandelbrot was thinking of when he chose the word fractal. Now, let's back up a little and take a look at the evolution of Fractals:

Go back to Top

BRIEF HISTORY OF FRACTALS

During the 1920's French Mathematicians Gaston Julia and Pierre Fatou discovered a set of mathematical rules while studying rational mappings of complex planes. They named these rules the "Julia Set". These rules (mappings) have center points (attractors) and edges (boundaries). One general feature of Julia sets is that the boundaries have self-similarity. That is, the boundary shape repeats over and over to what looks like infinity. Julia sets are, in turn, generated by Newton's root finding algorithms and may be expressed as 1-z³.

Below is what a classic Newton Fractal looks like both with and without color assignments. Note the 3 points in yellow on the blue fractal that are found in the expression for the power to the 3rd. This is why there are three branches in this picture. If it were to the power of 4, there would be four branches and so on:

In 1967 Polish-born Benoit Mandelbrot, Ph.D in Mathematics investigated the idea of measuring the length of a coastline. He concluded that was pointless to use standard Euclidean single-line geometry to measure something in a three-dimensional world. He said that rather than having a natural number dimension, it has a "fractional dimension." During the 1970's was studying the P.F. Verhulst process which involves the idea of deterministic chaos and discovered a set of rules which he named after himself the "Mandelbrot Set". It revealed some universal aspects of complex dynamical processes in an elementary way: Certain behaviors are typical and are found in a variety of systems. These rules identify principles that show relations between individual scenarios. They embody a principle of the transition from order to chaos. The basic Mandelbrot is expressed: F = x² + c. He did two basic things different from the Verhulst process: he looked at complex numbers instead of real numbers, and on a plane rather than on a line.

In the Fall of 1981 a collaboration between Mathematicians and Physicists was formed at a workshop for the study of Chaotic Dynamics at the University of Bremen, Germany. This led to further study of fractals and eventually to a very successful and popular brochure titled "Harmonie in Chaos und Kosmos". From that success came the first public exhibition of the "fractal art" in January 1984, also in Germany.

Go back to Top

HOW IT IS DONE (THE MATH PART)

Both Mandlebrot Set and Julia Sets have basic shapes and attributes. They both have at least one point and they both have a boundary. The basic shape may look something like this:

Very generally speaking a Mandlebrot has one point and a smooth boundary around it. A Julia has many points and the boundaries end up connecting with each other.

The following is how a basic Mandlebrot Set can be created:
The computer starts by putting an invisible complex-number coordinate system on the computer screen. Every point in this complex plane is processed in the following way:

1. Substitute the coordinates of the point into the expression x² + c for x.
2. Take the result of step 1 and substitute it back into the expression for x again. (Each time this is done is called an iteration.)
3. Keep repeating this process until the value of the expression reaches 2.0, or a preset number of iterations is reached.
4. Give the point a color determined by how many iterations it took for the value to exceed 2.0. If the preset number if iterations is reached before the value reaches 2.0 then the point is colored black.

An example would be:

Formula:
X² + c = c (C has to be a complex number, so we can plug in (1 + 2i)).
0² + (1 + 2i) = 1 + 2i

(1 + 2i)² + (1 + 2i) = -3 + 4i (see below how to do this step)
1 + 2i + 2i +4i² (since i² -1) = 1 + 4i -4 = -3 + 4i

Any point in the black region has a magnitude less than or equal to 2, no matter how many iterations you do. The magnitude of -3 + 4i = sq. root (-3)² = 4, = sq. root 9 + 16, = sq. root 25, = 5. Five is the answer, so since it's not equal to or less than 2, the magnitude of (1 + 2i)² is not in the Mandlebrot Set. It's outside the set, so it is assigned a color other than black.

This is only one iteration. To get a complete picture with lots of colors you might have to do between 10 to many millions of iterations!

This might be the result:
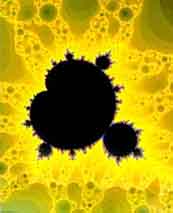
What is the difference between Julia sets and Mandelbrot set? Each point of the complex plane is associated with a Julia set, so you can think to the Mandelbrot set as an "index" for Julia sets: Each point of the Mandelbrot set is associated with a particular Julia set. The process to build a Julia set is the same used for the Mandelbrot set. The only difference is that for the Julia set X is fixed, while C varies. The classic Julia might look like this:

Mandelbrot began with the mathematically equivalent Verhulst process, but added a complex number instead of a whole number: x_n+1 = f(x_n) = x²_n + c. This produces the basic Mandelbrot Set which has a round shape and one bulb. The point x_n tells where the point is supposed to go in the plane (as opposed to on the line as in the Verhulst process). This reiteration will produce a basic Mandelbrot Set shape, but with two bulbs. This reiteration cycle can be repeated always producing one less bulb than the power you raise x to.

This is an example of Z = x³ + c:

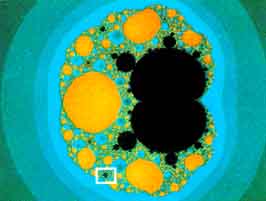
In very simplistic and basic terms this is what produces the beauty that we see in the computer-generated fractal images.

Go back to Top

MATH GLOSSARY

Chaos

The branch of mathematics that studies small changes in the beginning phases of a system that will make wide and varied results.

Complex Numbers

A number of the form a + bi, where a and b are real numbers and i is an imaginary number.

Dynamical Systems

A branch of mathematics that studies how complex systems change over time.

Equation

A statement that two algebraic expressions are equal.

Expression

A statement or one half of an equation.

Mappings

Connections between x and y values, like functions.

Natural Numbers

The set of natural numbers is {1,2,3,4...}

Polynomial

A term or the sum of a finite number of terms.

Real Numbers

The set of real numbers is {x|x is a number that can be represented by a point on the number line}.

Go back to Top

INTERESTING WEB SITES